
【题目】如图,L1,L2分别表示一种白炽灯和一种节能灯的费用y(费用=灯的售价+电费,单位:元)与照明时间x(h)的函数图像,假设两种灯的使用寿命都是2000h,照明效果一样.
(1)根据图像分别求出L1,L2的函数关系式.
(2)当照明时间为多少时,两种灯的费用相等?
(3)小亮房间计划照明2500h,他买了一个白炽灯和一个节能灯,请你帮他设计最省钱的用灯方法(直接给出答案,不必写出解答过程).

【答案】(1)y2=0.012x+20(0≤x≤2000).(2)当照明时间为1000h时,两种灯的费用相等.(3)节能灯使用2000h,白炽灯使用500h.
【解析】
(1)根据l1经过点(0,2)、(500,17),得方程组解之可求出解析式,同理l2过(0,20)、(500,26),易求解析式;
(2)费用相等即y1=y2,解方程求出时间;
(3)求出交点坐标,结合函数图象回答问题.
(1)设L1的解析式为y1=k1x+b1,L2的解析式为y2=k2x+b2,
由图可知L1过点(0,2),(500,17),
∴![]()
∴k1=0.03,b1=2,
∴y1=0.03x+2(0≤x≤2000),
由图可知L2过点(0,20),(500,26),
同理y2=0.012x+20(0≤x≤2000);
(2)若两种费用相等,
即y1=y2,
则0.03x+2=0.012x+20,
解得x=1000,
∴当x=1000时,两种灯的费用相等;
(3)时间超过1000小时,故前2000h用节能灯,剩下的500h,用白炽灯.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】点A在数轴上对应的数为a,点B对应的数为b,且a,b满足:|a+3|+(b-2)2=0
(1)求线段AB的长;
(2)如图①,点C在数轴上对应的数为x,且是方程![]() 的根,在数轴上是否存在点M使MA+MB=
的根,在数轴上是否存在点M使MA+MB=![]() BC+AB?若存在,求出点M对应的数;若不存在,说明理由;
BC+AB?若存在,求出点M对应的数;若不存在,说明理由;
(3)如图②,若N点是B点右侧一点,NA的中点为Q,P为NB的三等分点且靠近于B点,当N在B的右侧运动时,请直接判断![]() 的值是不变的还是变的,如果不变请直接写出其值,如果是变的请说明理由.
的值是不变的还是变的,如果不变请直接写出其值,如果是变的请说明理由.
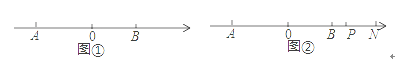
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,I点为△ABC的内心,D点在BC上,且ID⊥BC,若∠B=44°,∠C=56°,则∠AID的度数为何?( )

A. 174 B. 176 C. 178 D. 180
查看答案和解析>>
科目:初中数学 来源: 题型:
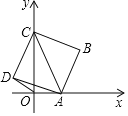
【题目】如图,点A是x轴上的一个动点,点C在y轴上,以AC为对角线画正方形ABCD,已知点C的坐标是![]() ,设点A的坐标为
,设点A的坐标为![]() .
.
![]() 当
当![]() 时,正方形ABCD的边长
时,正方形ABCD的边长![]() ______.
______.
![]() 连结OD,当
连结OD,当![]() 时,
时,![]() ______.
______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小明想探究函数![]() 的性质,他借助计算器求出了y与x的几组对应值,并在平面直角坐标系中画出了函数图象:
的性质,他借助计算器求出了y与x的几组对应值,并在平面直角坐标系中画出了函数图象:
x | … | -3 | -2 | -1 | 1 | 2 | 3 | … |
y | … | 2.83 | 1.73 | 0 | 0 | 1.73 | 2.83 | … |

小聪看了一眼就说:“你画的图象肯定是错误的.”
请回答:小聪判断的理由是_____________.请写出函数![]() 的一条性质:_____________.
的一条性质:_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOC为直角,OC是∠BOD的平分线,且∠AOB=57.65°,则∠AOD的度数是( )
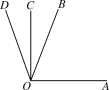
A. 122°20′ B. 122°21′ C. 122°22′ D. 122°23′
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在篮球比赛中,某队员连续10场比赛中每场的得分情况如下所示:
场次(场) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
得分(分) | 13 | 4 | 13 | 16 | 6 | 19 | 4 | 4 | 7 | 18 |
则这10场比赛中该队员得分的中位数和众数分别是( )
A.10,4
B.10,13
C.11,4
D.12.5,13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是由几个相同的小正方体搭成的几何体,
(1)搭成这个几何体需要 个小正方体;
(2)画出这个几何体的主视图和左视图;
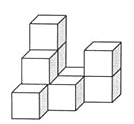
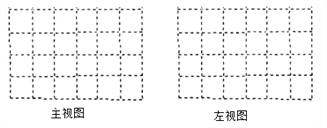
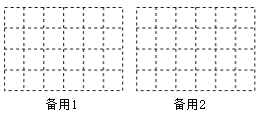
(3)在保持主视图和左视图不变的情况下,最多可以拿掉n个小正方体,则n= ,请在备用图中画出拿掉n个小正方体后新的几何体的俯视图.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com