
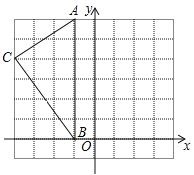
【题目】已知,如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数![]() (n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D,若OB=2OA=3OD=6.
(n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D,若OB=2OA=3OD=6.
(1)求一次函数与反比例函数的解析式;
(2)求两函数图象的另一个交点坐标;
(3)直接写出不等式;![]() 的解集.
的解集.

【答案】(1)y=﹣2x+6,![]() ;(2)(5,﹣4);(3)﹣2≤x<0或x≥5.
;(2)(5,﹣4);(3)﹣2≤x<0或x≥5.
【解析】
试题分析:(1)先求出A、B、C坐标,再利用待定系数法确定函数解析式.
(2)两个函数的解析式作为方程组,解方程组即可解决问题.
(3)根据图象一次函数的图象在反比例函数图象的下方,即可解决问题,注意等号.
试题解析:(1)∵OB=2OA=3OD=6,∴OB=6,OA=3,OD=2,∵CD⊥OA,∴DC∥OB,∴![]() ,∴
,∴![]() ,∴CD=10,∴点C坐标(﹣2,10),B(0,6),A(3,0),∴
,∴CD=10,∴点C坐标(﹣2,10),B(0,6),A(3,0),∴![]() 解得:
解得:![]() ,∴一次函数为y=﹣2x+6.
,∴一次函数为y=﹣2x+6.
∵反比例函数![]() 经过点C(﹣2,10),∴n=﹣20,∴反比例函数解析式为
经过点C(﹣2,10),∴n=﹣20,∴反比例函数解析式为![]() ;
;
(2)由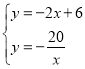 ,解得
,解得![]() 或
或![]() ,故另一个交点坐标为(5,﹣4);
,故另一个交点坐标为(5,﹣4);
(3)由图象可知![]() 的解集:﹣2≤x<0或x≥5.
的解集:﹣2≤x<0或x≥5.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
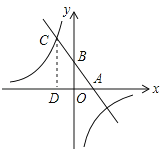
【题目】探究(1)如图1,把△ABC沿DE折叠,使点A落在点A’处,请你判断∠1+∠2与∠A的关系?直接写出结论,不必说明理由.
思考(2)如图2,BI平分∠ABC,CI平分∠ACB,把△ABC折叠,使点A与点I重合,若∠1+∠2=130°,求∠BIC的度数;
应用(3)如图3,在锐角△ABC中,BF⊥AC于点F,CG⊥AB于点G,BF、CG交于点H,把△ABC折叠使点A和点H重合,试探索∠BHC与∠1+∠2的关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
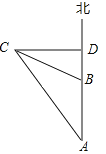
【题目】如图,下午2时一艘轮船从A处向正北方向航行,5时达到B处,继续航行到达D处时发现,灯塔C恰好在正西方向,从A处、B处望灯塔C的角度分别是∠A=30°,∠DBC=60°,已知轮船的航行速度为24海里/时,求AD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在平面直角坐标系的坐标分别为A(﹣1,5),B(﹣1,0),C(﹣4,3),按要求完成:
(1)在同一坐标系中,画出△ABC关于y轴对称的图形△A'B'C';
(2)若CD是△ABC中AB边的中线,E是CD的中点,F是AE的中点,连接AE、BE,FB,则△EFB的面积S= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB、BC的垂直平分线相交于三角形内一点O,下列结论中,错误的是( )
A. 点O在AC的垂直平分线上
B. △AOB、△BOC、△COA都是等腰三角形
C. ∠OAB+∠OBC+∠OCA=90°
D. 点O到AB、BC、CA的距离相等
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com