
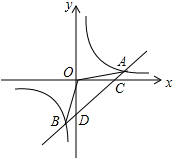
 如图,一次函数y=x+b和反比例函数$y=\frac{k}{x}(k≠0)$交于点A(2,1).
如图,一次函数y=x+b和反比例函数$y=\frac{k}{x}(k≠0)$交于点A(2,1).分析 (1)把A的坐标代入反比例函数$y=\frac{k}{x}(k≠0)$能求出反比例函数的解析式,把A的坐标代入一次函数y=x+b求出一次函数的解析式;
(2)求出D的坐标,分别求出△AOD和△BOD的面积,即可求出答案.
(3)根据函数的图象求得即可.
解答 解:(1)∵反比例函数$y=\frac{k}{x}(k≠0)$的图象过点A(2,1),
∴1=$\frac{k}{2}$,即k=2,
∴反比例函数的解析式为:y=$\frac{2}{x}$.
∵一次函数y=x+b(k≠0)的图象过点A(2,1),
∴1=2+b,解得b=-1,
∴一次函数的解析式为:y=x-1.
(2)∵令x=0,则y=-1,
∴D(0,-1),
即DO=1,
解$\frac{2}{x}$=x-1,
解得x=-1,
∴B(-1,-2),
∴S△AOB=S△AOD+S△BOD
=$\frac{1}{2}$×1×1+$\frac{1}{2}$×1×2=$\frac{3}{2}$.
(3)∵A(2,1),B(-1,-2),
∴一次函数的值大于反比例函数的值的x的取值范围为:-1<x<0或x>2.
点评 本题考查了反比例函数与一次函数的交点问题,用待定系数法求一次函数和反比例函数的解析式,三角形的面积等知识点的综合应用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
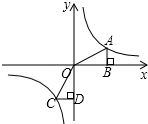 如图,A,C是函数$y=\frac{1}{x}$的图象上任意两点,过A作x轴的垂线,垂足为B,过C作y轴的垂线,垂足为D,记Rt△OAB的面积为S1,Rt△COD的面积S2,则( )
如图,A,C是函数$y=\frac{1}{x}$的图象上任意两点,过A作x轴的垂线,垂足为B,过C作y轴的垂线,垂足为D,记Rt△OAB的面积为S1,Rt△COD的面积S2,则( )| A. | S1>S2 | B. | S1=S2 | C. | S1<S2 | D. | S1≥S2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
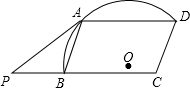 如图,在?ABCD中,∠ABC=70°,半径为r的⊙O经过点A,B,D,$\widehat{AD}$的长是$\frac{πr}{2}$,延长CB至点P,使得PB=AB.判断直线PA与⊙O的位置关系,并说明理由.
如图,在?ABCD中,∠ABC=70°,半径为r的⊙O经过点A,B,D,$\widehat{AD}$的长是$\frac{πr}{2}$,延长CB至点P,使得PB=AB.判断直线PA与⊙O的位置关系,并说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com