
初三年级某班有54名学生,所在教室有6行9列座位,用 表示第
表示第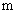 行第
行第 列的座位,新学期准备调整座位,设某个学生原来的座位为
列的座位,新学期准备调整座位,设某个学生原来的座位为 ,如果调整后的座位为
,如果调整后的座位为 ,则称该生作了平移
,则称该生作了平移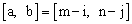 ,并称
,并称 为该生的位置数。若当
为该生的位置数。若当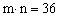 时,
时,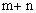 取得最小值,则该生位置数的最大值为 。
取得最小值,则该生位置数的最大值为 。
科目:初中数学 来源: 题型:
如图,已知直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,AB=8,CD=10 .
.
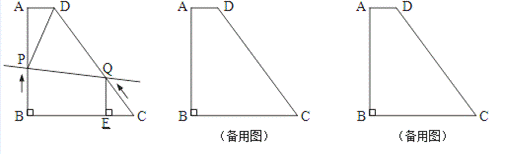

(1)求梯形ABCD的面积;
(2)动点P从点B出发,以2个单位/s的速度沿B→A→D→C方向向点C运动;动点Q从点C出发,以2个单位/s的速度沿 C→D→A方向向点A运动;过点Q作QE
C→D→A方向向点A运动;过点Q作QE ⊥BC于点E.若P、Q两点同时出发,当其中一点到达终点时另一点也随之停止运动,设运动时间为t秒.问:
⊥BC于点E.若P、Q两点同时出发,当其中一点到达终点时另一点也随之停止运动,设运动时间为t秒.问:
①当点P在B→A上运动时,是否存在这样的t,使得直线PQ将梯形ABCD的周长平分 ?若存在,请求出t的值
?若存在,请求出t的值 ,并判断此时PQ是否平分梯形ABCD的面积;若不存在,请说明理由.
,并判断此时PQ是否平分梯形ABCD的面积;若不存在,请说明理由.
②在运动过程中,是否存在这样的t,使得以P、D、Q为顶点的三角形恰好是以DQ为一腰的等腰三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
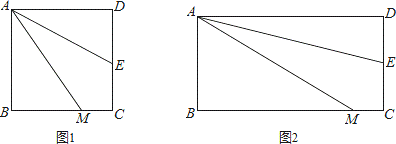
【问题情境】如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
【探究展示】
(1)证明:AM=AD+MC;
(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请 说明理由.
说明理由.
【拓展延伸】
(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
阅读下面的材料:
小明在数学课外小组活动中遇到这样一个“新定义”问题 :
:
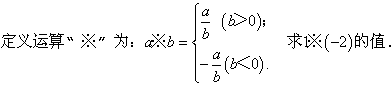

小明是这样解 决问题的:由新定义可知a=1,b=-2,又b<0,所以1※(-2)=
决问题的:由新定义可知a=1,b=-2,又b<0,所以1※(-2)=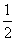
 .
.
请你参考小明的解题思路,回答下列问题:
(1)计算:2※3= ;
(2)若5※m=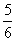
 ,则m= .
,则m= .
(3) 函数y=2※x(x≠0)的图象大致是(
函数y=2※x(x≠0)的图象大致是( )
)


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com