
【题目】已知:如图,在ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF. 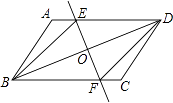
(1)求证:△DOE≌△BOF;
(2)当∠DOE等于多少度时,四边形BFDE为菱形?请说明理由.
【答案】
(1)证明:∵在ABCD中,O为对角线BD的中点,
∴BO=DO,∠EDB=∠FBO,
在△EOD和△FOB中
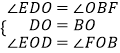 ,
,
∴△DOE≌△BOF(ASA)
(2)解:当∠DOE=90°时,四边形BFDE为菱形,
理由:∵△DOE≌△BOF,
∴OE=OF,
又∵OB=OD
∴四边形EBFD是平行四边形,
∵∠EOD=90°,
∴EF⊥BD,
∴四边形BFDE为菱形.
【解析】(1)利用平行四边形的性质以及全等三角形的判定方法得出△DOE≌△BOF(ASA);(2)首先利用一组对边平行且相等的四边形是平行四边形得出四边形EBFD是平行四边形,进而利用垂直平分线的性质得出BE=ED,即可得出答案.
【考点精析】掌握平行四边形的性质和菱形的判定方法是解答本题的根本,需要知道平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形.


科目:初中数学 来源: 题型:
【题目】动手操作: 如图①是一个长为2a,宽为2b的长方形,沿图中的虚线剪开分成四个大小相等的长方形,然后按照图②所示拼成一个正方形.
提出问题: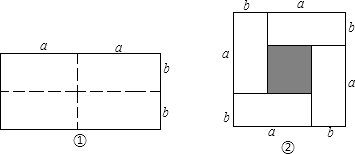
(1)观察图②,请用两种不同的方法表示阴影部分的面积;
(2)请写出三个代数式(a+b)2 , (a﹣b)2 , ab之间的一个等量关系. 问题解决:
根据上述(2)中得到的等量关系,解决下列问题:
已知:x+y=6,xy=3.求:(x﹣y)2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:31+1=4,32+1=10,33+1=28,34+1=82,35+1=244,…,归纳各计算结果中的个位数字的规律,猜测32017+1的个位数字是( )
A.0
B.2
C.4
D.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com