
【题目】某水果店总共筹备了5.1万资金计划购入一些时令水果销售(品种及价格如下表所示).现租用一辆载货量2.4吨的小货车进货(租金600元),要求将余下资金全部用于采购水果并使得所购水果装满货车.问应该怎样安排进货才能使水果店在销售完这批水果后获利最多?此时最大销售利润为多少元?
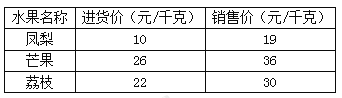
【答案】进货750千克凤梨和1650千克芒果可以使得销售利润最高为23250元
【解析】
试题分析:首先设进货凤梨x千克,芒果y千克,荔枝z千克,根据题意得出y和z的值,然后根据x≥0,y≥0,z≥0求出x的取值范围,然后求出总利润与x的函数关系式,根据一次函数的性质得出最值.
试题解析:设进货凤梨x千克,芒果y千克,荔枝z千克,
由题意可得:![]()
解得:![]()
由![]() 得:
得:
解得200≤x≤750
设销售利润为W,则W=9x+10y+8z=9x+10(3x-600)+8(3000-4x)=7x+18000
∵k=7>0,∴W随x的增大而增大,
当x=750时,w最大值=23250,
此时x=750,y=1650,z=0
即安排进货750千克凤梨和1650千克芒果可以使得销售利润最高为23250元.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】四舍五入法按要求对0.05019分别取近似值,其中错误的是( )
A. 0.1(精确到0.1), B. 0.05(精确到百分位),
C. 0.050(精确到百分位), D. 0.0502(精确到0.0001)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作:将一把三角尺放在边长为1的正方形ABCD上,并使它的直角顶点P在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于点Q,设A、P两点间的距离为x.

探究:
(1)当点Q在边CD上时,线段PQ与线段PB之间有怎样的大小关系?试证明你观察到的结论;
(2)当点Q在边CD上时,设四边形PBCQ的面积为y,求y与x之间的函数关系式,并写出x的取值范围;(3)当点P在线段AC上滑动时,△PCQ是否能成为等腰三角形?如果可能,指出所有能使△PCQ成为等腰三角形的点Q的位置,并求出相应x的值;如果不可能,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班五位同学的身高分别是156,160,158,166,160(单位:厘米),这组数据中,下列说法错误的是( )
A. 平均数是160 B. 众数是160
C. 中位数是160 D. 极差是160
查看答案和解析>>
科目:初中数学 来源: 题型:
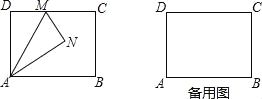
【题目】如图,矩形ABCD中,AB=4,AD=3,M是边CD上一点,将△ADM沿直线AM对折,得到△ANM.
(1)当AN平分∠MAB时,求DM的长;
(2)连接BN,当DM=1时,求△ABN的面积;
(3)当射线BN交线段CD于点F时,求DF的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com