
【题目】如图,矩形ABCD中,AB=4,AD=3,M是边CD上一点,将△ADM沿直线AM对折,得到△ANM.
(1)当AN平分∠MAB时,求DM的长;
(2)连接BN,当DM=1时,求△ABN的面积;
(3)当射线BN交线段CD于点F时,求DF的最大值.
【答案】(1)DM=![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)由折叠可知:△ANM≌△ADM,∠MAN=∠DAM,由AN平分∠MAB,得到∠MAN=∠NAB,进一步有∠DAM=∠MAN=∠NAB.由四边形ABCD是矩形,得到∠DAM=30°,由DM=ADtan∠DAM得到DM的长;
(2)如图1,延长MN交AB延长线于点Q,∵由四边形ABCD是矩形,得到∠DMA=∠MAQ.由折叠可知:△ANM≌△ADM,∠DMA=∠AMQ,得到∠MAQ=∠AMQ,故MQ=AQ.
设NQ=x,则AQ=MQ=1+x.在Rt△ANQ中,由![]() ,得到x=4.
,得到x=4.
故NQ=4,AQ=5,由![]() =
=![]() =
=![]() ANNQ,即可得到结论;
ANNQ,即可得到结论;
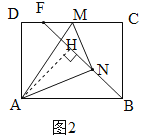
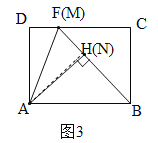
(3)如图2,过点A作AH⊥BF于点H,则△ABH∽△BFC,故![]() .由AH≤AN=3,AB=4,故当点N、H重合(即AH=AN)时,DF最大.此时M、F重合,B、N、M三点共线,△ABH≌△BFC(如图3),而CF=BH=
.由AH≤AN=3,AB=4,故当点N、H重合(即AH=AN)时,DF最大.此时M、F重合,B、N、M三点共线,△ABH≌△BFC(如图3),而CF=BH=![]() =
=![]() ,故课求出DF的最大值.
,故课求出DF的最大值.
试题解析:(1)由折叠可知:△ANM≌△ADM,∴∠MAN=∠DAM,∵AN平分∠MAB,∴∠MAN=∠NAB,∴∠DAM=∠MAN=∠NAB.∵四边形ABCD是矩形,∴∠DAB=90°,∴∠DAM=30°,∴DM=ADtan∠DAM=![]() =
=![]() ;
;
(2)如图1,延长MN交AB延长线于点Q,∵四边形ABCD是矩形,∴AB∥DC,∴∠DMA=∠MAQ.由折叠可知:△ANM≌△ADM,∴∠DMA=∠AMQ,AN=AD=3,MN=MD=1,∴∠MAQ=∠AMQ,∴MQ=AQ.
设NQ=x,则AQ=MQ=1+x.在Rt△ANQ中, ![]() ,∴
,∴![]() ,解得:x=4.
,解得:x=4.
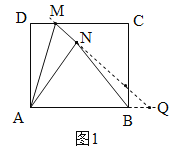
∴NQ=4,AQ=5,∵AB=4,AQ=5,∴![]() =
=![]() =
=![]() ANNQ=
ANNQ=![]() ;
;
(3)如图2,过点A作AH⊥BF于点H,则△ABH∽△BFC,∴![]() .∵AH≤AN=3,AB=4,∴当点N、H重合(即AH=AN)时,DF最大.(AH最大,BH最小,CF最小,DF最大)
.∵AH≤AN=3,AB=4,∴当点N、H重合(即AH=AN)时,DF最大.(AH最大,BH最小,CF最小,DF最大)
此时M、F重合,B、N、M三点共线,△ABH≌△BFC(如图3),∴CF=BH=![]() =
=![]() =
=![]() ,∴DF的最大值为:
,∴DF的最大值为:![]() .
.


 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 正投影是中心投影的一种特例
B. 正投影是平行投影的一种特例
C. 正投影既不是平行投影又不是中心投影
D. 平行投影就是正投影
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家快递公司,今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件,现假定该公司每月投递的快递总件数的增长率相同,求该快递公司投递总件数的月平均增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店总共筹备了5.1万资金计划购入一些时令水果销售(品种及价格如下表所示).现租用一辆载货量2.4吨的小货车进货(租金600元),要求将余下资金全部用于采购水果并使得所购水果装满货车.问应该怎样安排进货才能使水果店在销售完这批水果后获利最多?此时最大销售利润为多少元?
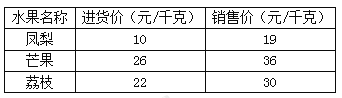
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
第1层 1+2=3
第2层 4+5+6=7+8
第3层 9+10+11+12=13+14+15
第4层 16+17+18+19+20=21+22+23+24
… …
在上述的数字宝塔中,从上往下数,2018在第_________层.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下各组线段为边,能组成三角形的是( )
A.2cm,4cm,6cm
B.8cm,6cm,4cm
C.14cm,6cm,7cm
D.2cm,3cm,6cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com