
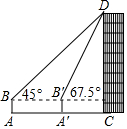
 如图,数学实践活动小组要测量学校附近楼房CD的高度,在水平地面A处安置测倾器测得楼房CD顶部点D的仰角为45°,向前走20米到达A′处,测得点D的仰角为67.5°,已知测倾器AB的高度为1.6米,则楼房CD的高度约为(结果精确到0.1米,$\sqrt{2}$≈1.414)( )
如图,数学实践活动小组要测量学校附近楼房CD的高度,在水平地面A处安置测倾器测得楼房CD顶部点D的仰角为45°,向前走20米到达A′处,测得点D的仰角为67.5°,已知测倾器AB的高度为1.6米,则楼房CD的高度约为(结果精确到0.1米,$\sqrt{2}$≈1.414)( )| A. | 34.14米 | B. | 34.1米 | C. | 35.7米 | D. | 35.74米 |
科目:初中数学 来源: 题型:填空题
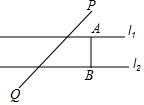 如图,已知直线l1∥l2,l1、l2之间的距离为8,点P到直线l1的距离为6,点Q到直线l2的距离为4,PQ=4$\sqrt{30}$,在直线l1上有一动点A,直线l2上有一动点B,满足AB⊥l2,且PA+AB+BQ最小,此时PA+BQ=16.
如图,已知直线l1∥l2,l1、l2之间的距离为8,点P到直线l1的距离为6,点Q到直线l2的距离为4,PQ=4$\sqrt{30}$,在直线l1上有一动点A,直线l2上有一动点B,满足AB⊥l2,且PA+AB+BQ最小,此时PA+BQ=16.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 售价x(元/千克) | 50 | 60 | 70 |
| 销售量y(千克) | 100 | 80 | 60 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
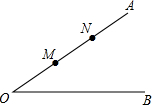 如图,∠AOB=45°,点M,N在边OA上,OM=x,ON=x+4,点P是边OB上的点.若使点P,M,N构成等腰三角形的点P恰好有三个,则x的值是x=0或x=4$\sqrt{2}$-4或4<x<4$\sqrt{2}$.
如图,∠AOB=45°,点M,N在边OA上,OM=x,ON=x+4,点P是边OB上的点.若使点P,M,N构成等腰三角形的点P恰好有三个,则x的值是x=0或x=4$\sqrt{2}$-4或4<x<4$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
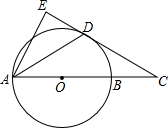 如图,AB是⊙O的直径,点C在AB的延长线上,AD平分∠CAE交⊙O于点D,且AE⊥CD,垂足为点E.
如图,AB是⊙O的直径,点C在AB的延长线上,AD平分∠CAE交⊙O于点D,且AE⊥CD,垂足为点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 186,188 | B. | 188,187 | C. | 187,188 | D. | 188,186 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
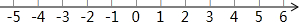
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com