
����Ŀ�����������
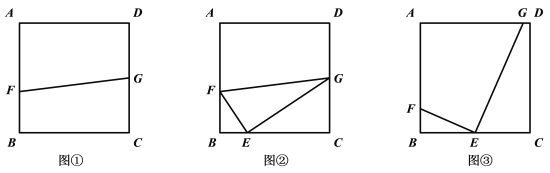
(1)��ͼ�٣���������![]() �У�
��![]() ����
����![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() �ϣ�����
�ϣ�����![]() ����
����![]() ��
��![]() ����
����![]() Ϊб�ߣ�������ֱ��������
Ϊб�ߣ�������ֱ��������![]() �����ڱ�
�����ڱ�![]() �ϴ��� ������������ֱ�Ƕ���
�ϴ��� ������������ֱ�Ƕ���![]() ��
��
����̽����
(2)��ͼ�ڣ���(1)�������£�![]() �Ƿ��������һ��ֱ��������
�Ƿ��������һ��ֱ��������![]() ����
����![]() �������
�������
��������
(3)ijС����һ���߳�Ϊ40�������λ����С����ҵ��һ��ǽ��![]() ����װ̨��������ü�������ӽ�Ϊ
����װ̨��������ü�������ӽ�Ϊ![]() �������������������ת�������ҿ��Լ�ظ������ÿһ���ط�����ͼ�ۣ�������
�������������������ת�������ҿ��Լ�ظ������ÿһ���ط�����ͼ�ۣ�������![]() �ǹ���
�ǹ���![]() ��һ��ˮƽ�棬
��һ��ˮƽ�棬![]() ��
��![]() ��������
��������![]() ��ͬһ��ƽ���ڣ�����
��ͬһ��ƽ���ڣ�����![]() ����
����![]() Ϊ
Ϊ![]()
![]() �������ֵ��
�������ֵ��
���𰸡�(1)2;(2)![]() ;(3)
;(3) ![]() ��������ֵΪ500����СֵΪ400.
��������ֵΪ500����СֵΪ400.
��������
(1) ��F��FH��DC��DC�ཻ��H,��BE=x���ֱ���Rt��GHF��Rt��BEF��Rt��ECG���ù��ɶ�����ʾFE2��EG2��FG2,����BC�ϴ��ڵ�Eʹ��![]() Ϊֱ�������Σ���������
Ϊֱ�������Σ���������![]() ��������ʽ��ΪһԪ���η��̣����ݷ��̵Ľ��������������ж������ĵ���������
��������ʽ��ΪһԪ���η��̣����ݷ��̵Ľ��������������ж������ĵ���������
��2�����ݣ�1���п����BE=1���ֱ����EF��EG�������![]() �������
�������
��3����G��AD�Ϻ�G��CD�������������.�ɽ������������ʾ![]() �����������a��ȡֵ��Χ�ɷֱ�
�����������a��ȡֵ��Χ�ɷֱ�![]() �����������ֵ����Сֵ.
�����������ֵ����Сֵ.
(1)��ͼ��F��FH��DC��DC�ཻ��H��
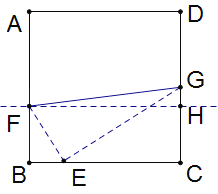
���FHC=��FHG=90��
���ı���![]() Ϊ�����Σ�
������
���B=��C=90����BC=AD=4��
���ı���![]() Ϊ���Σ�
����
��![]() ,FH=BC=4.
,FH=BC=4.
��![]() ��
��
��![]()
��Rt��GHG�и��ݹ��ɶ���
![]() .
.
����BC�ϴ���E����BE=x����EC=4-x.
����Rt��BEF��Rt��ECG�и��ݹ��ɶ���
![]() ��
��
![]() .
.
Ҫʹ��EFGΪֱ�������Σ�����ݹ��ɶ������涨��
![]() ��
��![]()
�����![]()
��![]()
��÷�������������ȵĽ⣬������������E��������
���2.
��2����![]() ��
��![]()
��![]()
��BE=1��
��ʱ![]() ����FE=
����FE=![]() ��
��
![]() ����
����![]()
��![]() �����=
�����=![]() .
.
(3)������������ۣ�
������ͼ����G����AD���˶�ʱ������FG����G����GH��BC����BC�ཻ��H.
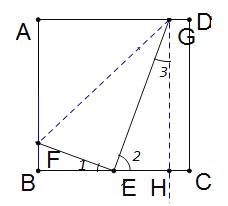
���GHE=90����
���2+��3=90����
��![]() ��
��
���1+��2=90����
���1=��3��
�ߡ�B=��GHE=90����
��Rt��BEF��Rt��HGE
��![]() ,
,
��BF=a����EH=2a
��EH��EC=20
��0��x��10
![]()
��ʱ����a=10ʱ��ȡ�����ֵ![]() .��a=0ʱ��ȡ����Сֵ
.��a=0ʱ��ȡ����Сֵ![]() .
.
������ͼ��![]() ʱ��G��CD��ʱ������FG��FG�е�OΪԲ����OFΪ�뾶��Բ��
ʱ��G��CD��ʱ������FG��FG�е�OΪԲ����OFΪ�뾶��Բ��
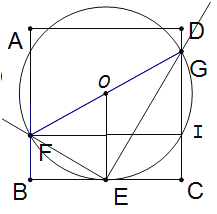
�ߡ�FEG=90����
��E���ڡ�O��
��BF=a��CG=b��
��EΪBC�е㣬FO=OG
��![]() ��
��
��FG=2OF=a+b
![]()
��FG//BCʱ����O�İ뾶��С����a+b��С��ʱa+b=FG=BC=40��![]() ��
��
���ͬ����֤Rt��BEF��Rt��CGE
��![]() ,��
,��![]()
��![]() ��a��b�ɷ�����������ϵ��
��a��b�ɷ�����������ϵ��
��O��DC�ཻ��I������FI��
���FIG=90��
�ߡ�B=��C=90��
���ı���BCIFΪ���Σ�
��IC=BF=a��GI=GC-IC=b-a
��Rt��FIG�У����ݹ��ɶ���
![]() ,��
,��![]()
�൱|b-a|���ʱa+b��ֵ���
��![]()
�൱a=10��b=40��a+b=50��
��a=40ʱ��b=10��a+b=50����ʱ![]() ������Ϊ500.
������Ϊ500.
�ۺϢ٢ڣ�![]() ��������ֵΪ500����СֵΪ400.
��������ֵΪ500����СֵΪ400.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
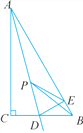
����Ŀ����ͼ����Rt��ABC������C��90�㣬��ABC��60�㣬D��BC���ϵĵ���CD��1������ACD��ֱ��AD��������C�պ�����AB���ϵĵ�E������P��ֱ��AD�ϵĶ���������PEB���ܳ�����Сֵ��______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
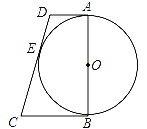
����Ŀ����ͼ��ʾ��AB����O��ֱ����AD����O�����ڵ�A��DE����O�����ڵ�E����CΪDE�ӳ�����һ������CE=CB��
��1����֤��BCΪ��O��������
��2����AB=4��AD=1�����߶�CE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijҩƷ�о�������һ�ֿ�����ҩ�������궯��ʵ�飬�״������ٴ��������飬��ó��˷�ҩ��ѪҺ��ҩ��Ũ��y����/���������ҩʱ��xСʱ֮�亯����ϵ��ͼ��ʾ����4��x��10ʱ��y��x�ɷ���������
��1������ͼ��ֱ����ѪҺ��ҩ��Ũ���������½���y��x֮��ĺ�����ϵʽ��
��2����ѪҺ��ҩ��Ũ�Ȳ�����2��/�����ij���ʱ�����Сʱ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
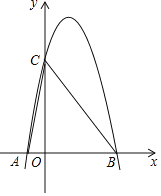
����Ŀ����֪����ͼ�����κ���![]() ��ͼ����
��ͼ����![]() �ύ��
�ύ��![]() ��
��![]() ���㣬��
���㣬��![]() �ύ�ڵ�
�ύ�ڵ�![]() ���Ҿ�����
���Ҿ�����![]()
(1)��������ߵĽ���ʽ����������ͶԳ��
(2)�����������Ƿ����һ��![]() ��ʹ
��ʹ![]() �������
�������![]() ��������(��
��������(��![]() �����
�����![]() �غ�)�������ڣ������
�غ�)�������ڣ������![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ����Ϊ48cm����˿�������Σ�����ÿһ����˿�ij���Ϊ�ܳ�����һ��������.
��1��Ҫʹ�����������ε����֮�͵���74cm2����ô�����˿�������κ�ij��ȷֱ��Ƕ���?
��2�����������ε����֮�Ϳ��ܵ���68cm2��?���ܣ����������˿�ij��ȣ������ܣ���˵������.
��3������ô��������ʹ�����������ε����֮��Ϊ��С����Сֵ�Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
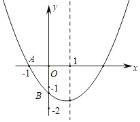
����Ŀ����ͼ����֪���κ���y��ax2+bx+c��a��0����ͼ����x�ύ�ڵ�A����1��0������y��Ľ���B�ڣ�0����2����C��0����1��֮�䣨�����������㣩���Գ���Ϊֱ��x��1�����н��ۣ���abc��0����4a+2b+c��0����4ac��b2��8a����![]() ����b��c�����к�������ȷ���۵�ѡ����_____��
����b��c�����к�������ȷ���۵�ѡ����_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ʵ�����е�һ�ְڶ�װ�ã�BC�ڵ����ϣ�֧��ABC�ǵױ�ΪBC�ĵ���ֱ�������Σ��ڶ���AD���Ƶ�A��ת���ڶ���DM���Ƶ�D��ת��AD��30��DM��10��
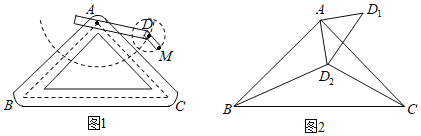
��1������ת�����У�
�ٵ�A��D��M������ͬһֱ����ʱ����AM�ij���
�ڵ�A��D��M����Ϊͬһֱ�������εĶ���ʱ����AM�ij���
��2�����ڶ���AD˳ʱ����ת90������D��λ������ABC��ĵ�D1ת�����ڵĵ�D2��������D1D2����ͼ2����ʱ��AD2C��135����CD2��60����BD2�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��![]() ��x�ᣬy��ֱ��ڵ�A����B��������
��x�ᣬy��ֱ��ڵ�A����B��������![]() ����A��B���
����A��B���![]() .
.
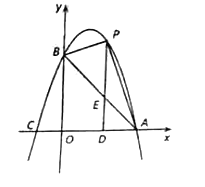
��1���������ߵĽ���ʽ��
��2����P��ֱ��AB�Ϸ�����������һ���㣨�����A��B�غϣ�������P��x��Ĵ��ߣ�����ΪD�����߶�AB�ڵ�E.���P�ĺ�����Ϊm.
����![]() �����y����m�ĺ�����ϵʽ����mΪ��ֵʱ��y�����ֵ�����ֵ�Ƕ��٣�
�����y����m�ĺ�����ϵʽ����mΪ��ֵʱ��y�����ֵ�����ֵ�Ƕ��٣�
������E�Ǵ��߶�PD�����ȷֵ㣬���P������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com