
【题目】如图,一次函数y=kx+b的图象与x轴的交点坐标为(2,0),则下列说法:
①y随x的增大而减小;②b>0;③关于x的方程kx+b=0的解为x=2;④不等式kx+b>0的解集是x>2.
其中说法正确的有_________(把你认为说法正确的序号都填上).
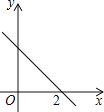
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,梯子斜靠在与地面垂直(垂足为O)的墙上,当梯子位于AB位置时,它与地面所成的角∠ABO=60°;当梯子底端向右滑动1m(即BD=1m)到达CD位置时,它与地面所成的角∠CDO=51°18′,求梯子的长. (参考数据:sin51°18′≈0.780,cos51°18′≈0.625,tan51°18′≈1.248)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段MN=8,C是线段MN上一动点,在MN的同侧分别作等边△CMD和等边△CNE.
(1)如图①,连接DN与EM,两条线段相交于点H,求证ME=DN,并求∠DHM的度数;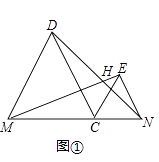
(2)如图②,过点D、E分别作线段MN的垂线,垂足分别为F、G,问:在点C运动过程中,DF+EG的长度是否为定值,如果是,请求出这个定值,如果不是请说明理由;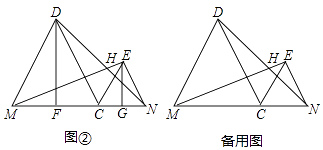
(3)当点C由点M移到点N时,点H移到的路径长度为(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个菱形![]() ,使
,使![]() ,连接
,连接![]() ,再以
,再以![]() 为边作第三个菱形
为边作第三个菱形![]() ,使
,使![]() ;…,按此规律所作的第六个菱形的边长为( )
;…,按此规律所作的第六个菱形的边长为( )

A. 9 B. ![]() C. 27 D.
C. 27 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个盒子里有完全相同的三个小球,球上分别标有数字﹣2,1,4.随机摸出一个小球(不放回),其数字为p,再随机摸出另一个小球其数字记为q,则满足关于x的方程x2+px+q=0有实数根的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD绕点A逆时针旋转30°,得到□AB′C′D′(点B′与点B是对应点,点C′与点C是对应点,点D′与点D是对应点),点B′恰好落在BC边上,则∠C=( )

A.155° B.170° C.105° D.145°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,点A,O,B分别表示-16,0,14,点P,Q分别从点A,B同时开始沿数轴正方向运动,点P的速度是每秒3个单位,点Q的速度是每秒1个单位,运动时间为t秒.若点P,Q,O三点在运动过程中,其中一点恰好是另外两点为端点构成的线段的三等分点时,则运动时间为_秒.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,AE∥CD,CE∥AB,连接DE交AC于点O. 
(1)证明:四边形ADCE为菱形;
(2)证明:DE=BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠D=∠BCD=90°,∠B=60°,AB=6,AD=9,点E是CD上的一个动点(E不与D重合),过点E作EF∥AC,交AD于点F(当E运动到C时,EF与AC重合),把△DEF沿着EF对折,点D的对应点是点G.设DE=x,△GEF与四边形ABCD重叠部分的面积为y.
(1)求CD的长及∠1的度数;
(2)若点G恰好在BC上,求此时x的值;
(3)求y与x之间的函数关系式,并求x为何值时,y的值最大?最大值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com