
如图,自来水公司的主管道从A小区向北偏东60°方向直线延伸,测绘员在A处测得要安装自来水的M小区在A小区北偏东30°方向,测绘员沿主管道测量出AC=200米,小区M位于C的北偏西60°方向,
(1)请你找出支管道连接点N,使得N到该小区铺设的管道最短.(在图中标出点N的位置)
(2)求出AN的长.

(1)作图见解析;(2)150米.
【解析】
试题分析:(1)由垂线段最短,可知过点M作MN⊥AC于点N,则此点N即为所求.
(2)由题意可首先求得∠AMC是直角,然后根据含30°的直角三角形的性质,即可求得答案.
(1)如图,过点M作MN⊥AC于点N,则点N即为所求.
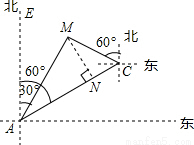
(2)如图:∵∠EAC=60°,∠EAM=30°,∴∠CAM=30°.∴∠AMN=60°.
又∵C处看M点为北偏西60°,∴∠MCB=30°.
∵∠EAC=60°,∴∠CAD=30°.∴∠BCA=30°.
∴∠MCA=∠MCB+∠BCA=60°.∴∠AMC=90°,∠MAC=30°.
∴MC=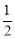 AC=
AC=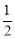 ×200=100(米),∠CMN=30°.
×200=100(米),∠CMN=30°.
∴NC=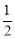 MC=50(米),
MC=50(米),
∴AN=AC-NC=200-50=150(米).
考点:1. 垂线段的性质;2. 解直角三角形的应用-方向角问题.


科目:初中数学 来源:2013-2014学年河南省中考调考二数学试卷(解析版) 题型:填空题
海安火车站的显示屏,每隔5分钟显示一次火车班次的信息,显示时间持续1分钟,某人到达该车站时,显示屏上正好显示火车班次信息的概率是
查看答案和解析>>
科目:初中数学 来源:2013-2014学年河北省保定市毕业生第一次模拟考试数学试卷(解析版) 题型:解答题
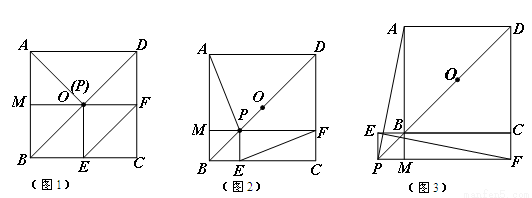
正方形ABCD中,点O是对角线DB的中点,点P在DB所在的直线上,PE⊥BC于E,PF⊥DC于F.
(1)如图1,当点P与点O重合时,延长FP交AB于点M,求证:AP=EF;
(2)如图2,当点P在线段DB上(不与点D、O、B重合)时,延长FP交AB于点M,求证:AP=EF;
(3)如图3,当点P在DB的延长线上时,请你猜想AP与EF的数量关系及位置关系,直接写出结论;若不成立,请写出相应的结论.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江西省九年级下学期期中模拟考试数学试卷(解析版) 题型:解答题
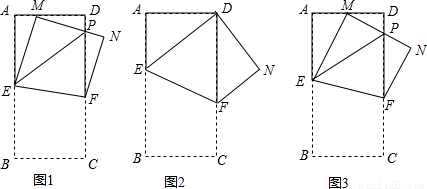
如图1,在矩形纸片ABCD中,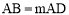 ,其中m≥1,将该矩形沿EF折叠(点E、F分别在边AB、CD上),使点B落在AD边上的点M处,点C落在点N处,MN与CD相交于点P,连接EP.设
,其中m≥1,将该矩形沿EF折叠(点E、F分别在边AB、CD上),使点B落在AD边上的点M处,点C落在点N处,MN与CD相交于点P,连接EP.设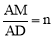 ,其中0<n≤1.
,其中0<n≤1.
(1)如图2,当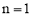 (即M点与D点重合),
(即M点与D点重合),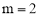 时,则
时,则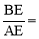 ;
;
(2)如图3,当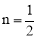 (M为AD的中点),m的值发生变化时,求证:
(M为AD的中点),m的值发生变化时,求证: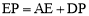 ;
;
(3)如图1,当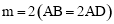 ,n的值发生变化时,
,n的值发生变化时,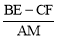 的值是否发生变化?说明理由.
的值是否发生变化?说明理由.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江西省九年级下学期期中模拟考试数学试卷(解析版) 题型:填空题
如图,□ABCD中,AC⊥AB. ,E是CD上的点,
,E是CD上的点, .点P从D点出发,以1cm/s的速度沿DA运动至A点停止.则当△EDP为等腰三角形时,点P的运动时间为 .
.点P从D点出发,以1cm/s的速度沿DA运动至A点停止.则当△EDP为等腰三角形时,点P的运动时间为 .

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江西省九年级下学期第一次段考数学试卷(解析版) 题型:填空题
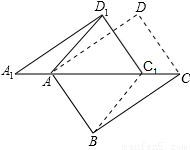
如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1、BC1。若∠ACB=30°,AB=1,CC1=x,△ACD与△A1C1D1重叠部分的面积为s,则下列结论:①△A1AD1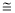 △CC1B;②当x=l时,四边形ABC1D1是菱形;③当x=2时,△BDD1为等边三角形;④
△CC1B;②当x=l时,四边形ABC1D1是菱形;③当x=2时,△BDD1为等边三角形;④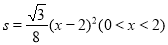 ;其中正确的是 (填序号)
;其中正确的是 (填序号)
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省中考一模数学试卷(解析版) 题型:选择题
下列图形中,既是轴对称图形,又是中心对称图形的是( )
A、矩形 B、平行四边形 C、角 D、等边三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com