
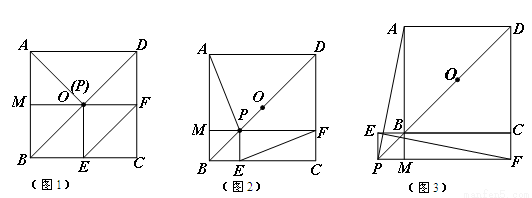
正方形ABCD中,点O是对角线DB的中点,点P在DB所在的直线上,PE⊥BC于E,PF⊥DC于F.
(1)如图1,当点P与点O重合时,延长FP交AB于点M,求证:AP=EF;
(2)如图2,当点P在线段DB上(不与点D、O、B重合)时,延长FP交AB于点M,求证:AP=EF;
(3)如图3,当点P在DB的延长线上时,请你猜想AP与EF的数量关系及位置关系,直接写出结论;若不成立,请写出相应的结论.
(1)证明见解析;(2)证明见解析;(3)AP=EF,且AP⊥EF.
【解析】
试题分析:(1)连接AC,则AC必过O点,延长FO交AB于M,由于O是BD中点,易证得△AOM≌△FOE,则AO=EF.
(2)方法与①类似,延长FP交AB于M,延长AP交BC于N,易证得四边形MBEP是正方形,可证得△APM≌△FEP,则AP=EF.
(3)解题思路和方法同(2).
试题解析:(1)如图1,
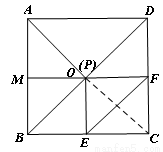
证明:连接AC,则AC必过点O,
∵四边形ABCD是正方形,AC是对角线.
∵OF⊥CD,FOM共线,
∵OM⊥AB,OE⊥BC.
∴∠ABE=∠BEO=∠BMO=90°
∴四边形OEBM是矩形.
∵AC平分∠BCD且OE⊥BC,OF⊥CD,
∴OF= OE
∴矩形OECF是正方形
∴∠MAO=∠OFE=∠AOM=∠OEF=45°,∠AMO=∠EOF=90°,
∴OM=OE=OF=AM
∴△AMO≌△FOE(AAS),
∴AP=EF.
(2)如图2,

∵PM⊥AB,PE⊥BC,∠MBE=90°,且∠MBP=∠EBP=45°,
∴四边形MBEP是正方形,
∴MP=PE,∠AMP=∠FPE=90°;
又∵AB﹣BM=AM,BC﹣BE=EC=PF,
且AB=BC,BM=BE,
∴AM=PF,
∴△AMP≌△FPE(SAS),
∴AP=EF.
(3)AP=EF,且AP⊥EF.
考点:1.正方形的性质;2.全等三角形的判定与性质.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源:2013-2014学年河南省驻马店市九年级上学期期末素质测试数学试卷(解析版) 题型:解答题
在平面直角坐标系中,∆ABC的顶点坐标是A(-7,1)、B(1,1)、C(1,7),线段DE的端点坐标是D(7,-1)、E(-1,-7)
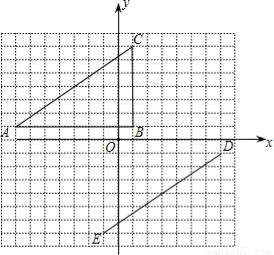
(1)试说明如何平移线段AC,使其与线段ED重合将线段AC先向______(上,下)平移_______个单位,再向_______(左,右)平移 _______个单位;
(2)将∆ABC绕坐标原点逆时针旋转,使AC的对应边为DE,请直接写出点B的对应点F的坐标;
(3)画出(2)中的∆DEF,并和∆ABC 同时绕坐标原点O逆时针旋转90o,画出旋转后的图形.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年河北省保定市毕业生第一次模拟考试数学试卷(解析版) 题型:填空题
如图,长方形ABCD中,M为CD中点,现在点B、M为圆心,分别以BC长、MC长为半径画弧,两弧相交于点P.若∠PMC=110°,则∠BPC的度数为 .

查看答案和解析>>
科目:初中数学 来源:2013-2014学年河北省保定市毕业生第一次模拟考试数学试卷(解析版) 题型:选择题
如图,已知AB是⊙O的直径,C是AB延长线上一点,BC=OB,CE是⊙O的切线,切点为D,过点A作AE⊥CE,垂足为E,则CD:CE的值是

A.2 B. 3 C. D.
D.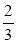
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江西省九年级下学期期中模拟考试数学试卷(解析版) 题型:解答题
如图,自来水公司的主管道从A小区向北偏东60°方向直线延伸,测绘员在A处测得要安装自来水的M小区在A小区北偏东30°方向,测绘员沿主管道测量出AC=200米,小区M位于C的北偏西60°方向,
(1)请你找出支管道连接点N,使得N到该小区铺设的管道最短.(在图中标出点N的位置)
(2)求出AN的长.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江西省九年级下学期第一次段考数学试卷(解析版) 题型:选择题
过正方体上底面的对角线和下底面一顶点的平面截去一个三棱锥所得到的几何体如图所示,它的俯视图为( )

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com