
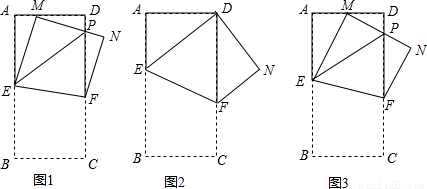
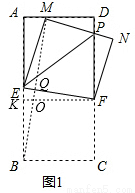
如图1,在矩形纸片ABCD中,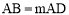 ,其中m≥1,将该矩形沿EF折叠(点E、F分别在边AB、CD上),使点B落在AD边上的点M处,点C落在点N处,MN与CD相交于点P,连接EP.设
,其中m≥1,将该矩形沿EF折叠(点E、F分别在边AB、CD上),使点B落在AD边上的点M处,点C落在点N处,MN与CD相交于点P,连接EP.设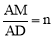 ,其中0<n≤1.
,其中0<n≤1.
(1)如图2,当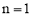 (即M点与D点重合),
(即M点与D点重合),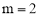 时,则
时,则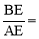 ;
;
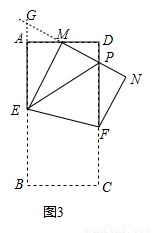
(2)如图3,当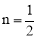 (M为AD的中点),m的值发生变化时,求证:
(M为AD的中点),m的值发生变化时,求证: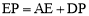 ;
;
(3)如图1,当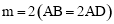 ,n的值发生变化时,
,n的值发生变化时,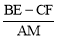 的值是否发生变化?说明理由.
的值是否发生变化?说明理由.
(1)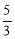 ;(2)证明见解析;(3)
;(2)证明见解析;(3)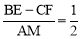 ,不发生变化,理由见解析.
,不发生变化,理由见解析.
【解析】
试题分析:(1)由条件可知,当n=1(即M点与D点重合),m=2时,AB=2AD,设AD=a,则AB=2a,由矩形的性质可以得出△ADE≌△NDF,就可以得出AE=NF,DE=DF,在Rt△AED中,由勾股定理就可以表示出AE的值,再求出BE的值就可以得出结论.
(2)延长PM交EA延长线于G,由条件可以得出△PDM≌△GAM,△EMP≌△EMG由全等三角形的性质就可以得出结论.
(3)如图1,连接BM交EF于点Q,过点F作FK⊥AB于点K,交BM于点O,通过证明△ABM∽△KFE,就可以得出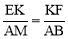 ,即
,即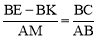 ,由AB=2AD=2BC,BK=CF就可以得出
,由AB=2AD=2BC,BK=CF就可以得出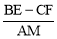 的值是
的值是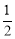 为定值.
为定值.
(1)∵四边形ABCD是矩形,∴AB=CD,AD=BC,∠A=∠B=∠C=∠D=90°.
∵AB=mAD,且n=2,∴AB=2AD.
∵∠ADE+∠EDF=90°,∠EDF+∠NDF=90°,∴∠ADE=∠NDF.
在△ADE和△NDF中,∠A=∠N,AD=ND,∠ADE=∠NDF,
∴△ADE≌△NDF(ASA).∴AE=NF,DE=DF.
∵FN=FC,∴AE=FC.
∵AB=CD,∴AB-AE=CD-CF. ∴BE=DF. ∴BE=DE.
Rt△AED中,由勾股定理,得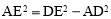 ,即
,即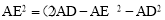 ,∴AE=
,∴AE=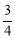 AD.
AD.
∴BE=2AD-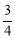 AD=
AD=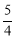 .
.
∴ .
.
(2)如图3,延长PM交EA延长线于G,∴∠GAM=90°.
∵M为AD的中点,∴AM=DM.
∵四边形ABCD是矩形,∴AB=CD,AD=BC,∠A=∠B=∠C=∠D=90°,AB∥CD.
∴∠GAM=∠PDM.
在△GAM和△PDM中,∠GAM=∠PDM,AM=DM,∠AMG=∠DMP,
∴△GAM≌△PDM(ASA).∴MG=MP.
在△EMP和△EMG中,PM=GM,∠PME=∠GME,ME=ME,
∴△EMP≌△EMG(SAS).∴EG=EP.
∴AG+AE=EP.∴PD+AE=EP,即EP=AE+DP.
(3)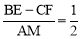 ,值不变,理由如下:
,值不变,理由如下:
如图1,连接BM交EF于点Q,过点F作FK⊥AB于点K,交BM于点O,
∵EM=EB,∠MEF=∠BEF,∴EF⊥MB,即∠FQO=90°.
∵四边形FKBC是矩形,∴KF=BC,FC=KB.
∵∠FKB=90°,∴∠KBO+∠KOB=90°.
∵∠QOF+∠QFO=90°,∠QOF=∠KOB,∴∠KBO=∠OFQ.
∵∠A=∠EKF=90°,∴△ABM∽△KFE.
∴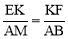 即
即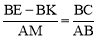 .
.
∵AB=2AD=2BC,BK=CF,∴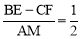 .
.
∴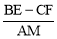 的值不变.
的值不变.
考点:1. 折叠问题;2.矩形的性质;3.全等三角形的判定和性质;4.勾股定理;5.相似三角形的判定和性质.


科目:初中数学 来源:2013-2014学年河南省中考调考二数学试卷(解析版) 题型:解答题
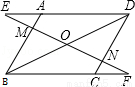
已知:如图在平行四边形ABCD中,过对角线BD的中点O作直线EF分别交DA的延长线、AB、DC、BC的延长线于点E、M、N、F.
(1)观察图形并找出一对全等三角形:△ ≌△ ,请加以证明;
(2)在(1)中你所找出的一对全等三角形,其中一个三角形可由另一个三角形经过怎样的变换得到?
查看答案和解析>>
科目:初中数学 来源:2013-2014学年河北省保定市毕业生第一次模拟考试数学试卷(解析版) 题型:选择题
如图,已知AB是⊙O的直径,C是AB延长线上一点,BC=OB,CE是⊙O的切线,切点为D,过点A作AE⊥CE,垂足为E,则CD:CE的值是

A.2 B. 3 C. D.
D.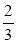
查看答案和解析>>
科目:初中数学 来源:2013-2014学年河北省保定市毕业生第一次模拟考试数学试卷(解析版) 题型:选择题
如果一个多边形的每个外角都等于36°,则这个多边形的边数是
A.4 B.6 C.8 D.10
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江西省九年级下学期期中模拟考试数学试卷(解析版) 题型:解答题
如图,自来水公司的主管道从A小区向北偏东60°方向直线延伸,测绘员在A处测得要安装自来水的M小区在A小区北偏东30°方向,测绘员沿主管道测量出AC=200米,小区M位于C的北偏西60°方向,
(1)请你找出支管道连接点N,使得N到该小区铺设的管道最短.(在图中标出点N的位置)
(2)求出AN的长.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江西省九年级下学期期中模拟考试数学试卷(解析版) 题型:填空题
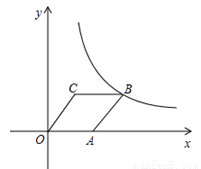
如图,菱形OABC的顶点C的坐标为(3,4).顶点A在x轴的正半轴上,反比例函数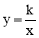 (x>0)的图象经过顶点B,则k的值为 .
(x>0)的图象经过顶点B,则k的值为 .
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江西省九年级下学期第一次段考数学试卷(解析版) 题型:解答题
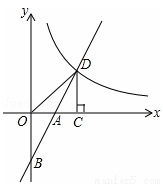
如图,在平面直角坐标系中,直线y=2x+b(b<0)与坐标轴交于A,B两点,与双曲线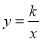 (x>0)交于D点,过点D作DC⊥x轴,垂足为C,连接OD。已知△AOB≌△ACD。
(x>0)交于D点,过点D作DC⊥x轴,垂足为C,连接OD。已知△AOB≌△ACD。
(1)如果b=-2,求k的值;
(2)试探究k与b的数量关系,并写出直线OD的解析式。
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省中考一模数学试卷(解析版) 题型:选择题
如图,△ABC的三个顶点分别在直线a、b上,且a∥b,若∠1=120°,∠2=80°,则∠3的度数是( )
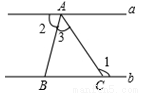
A.40° B.60° C.80° D.120°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com