
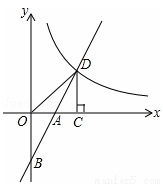
如图,在平面直角坐标系中,直线y=2x+b(b<0)与坐标轴交于A,B两点,与双曲线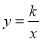 (x>0)交于D点,过点D作DC⊥x轴,垂足为C,连接OD。已知△AOB≌△ACD。
(x>0)交于D点,过点D作DC⊥x轴,垂足为C,连接OD。已知△AOB≌△ACD。
(1)如果b=-2,求k的值;
(2)试探究k与b的数量关系,并写出直线OD的解析式。
(1)4; (2)y=x.
【解析】
试题分析:(1)首先求出直线y=2x-2与坐标轴交点的坐标,然后由△AOB≌△ACD得到CD=OB,AO=AC,即可求出D坐标,由点D在双曲线y=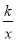 ( x>0)的图象上求出k的值;
( x>0)的图象上求出k的值;
(2)首先直线y=2x+b与坐标轴交点的坐标为A(-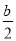 ,0),B(0,b),再根据△AOB≌△ACD得到CD=DB,AO=AC,即可求出D坐标,把D点坐标代入反比例函数解析式求出k和b之间的关系,进而也可以求出直线OD的解析式.
,0),B(0,b),再根据△AOB≌△ACD得到CD=DB,AO=AC,即可求出D坐标,把D点坐标代入反比例函数解析式求出k和b之间的关系,进而也可以求出直线OD的解析式.
(1)当b=-2时,
直线y=2x-2与坐标轴交点的坐标为A(1,0),B(0,-2).
∵△AOB≌△ACD,
∴CD=OB,AO=AC,
∴点D的坐标为(2,2).
∵点D在双曲线y=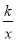 ( x>0)的图象上,
( x>0)的图象上,
∴k=2×2=4.
(2)直线y=2x+b与坐标轴交点的坐标为A(-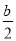 ,0),B(0,b).
,0),B(0,b).
∵△AOB≌△ACD,
∴CD=OB,AO=AC,
∴点D的坐标为(-b,-b).
∵点D在双曲线y=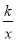 ( x>0)的图象上,
( x>0)的图象上,
∴k=(-b)•(-b)=b2.
即k与b的数量关系为:k=b2.
直线OD的解析式为:y=x.
考点:反比例函数综合题.


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源:2013-2014学年河北省邯郸市九年级中考二模数学试卷(解析版) 题型:选择题
如图,圆柱底面半径为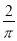 cm,高为9cm,点A、B分别是圆柱两底面圆周上的点,且A、B在同一母线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为
cm,高为9cm,点A、B分别是圆柱两底面圆周上的点,且A、B在同一母线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为
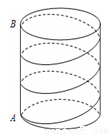
A.12cm B.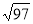 cm C.15 cm D.
cm C.15 cm D.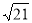 cm
cm
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江西省九年级下学期期中模拟考试数学试卷(解析版) 题型:解答题
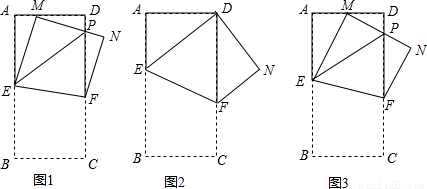
如图1,在矩形纸片ABCD中,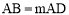 ,其中m≥1,将该矩形沿EF折叠(点E、F分别在边AB、CD上),使点B落在AD边上的点M处,点C落在点N处,MN与CD相交于点P,连接EP.设
,其中m≥1,将该矩形沿EF折叠(点E、F分别在边AB、CD上),使点B落在AD边上的点M处,点C落在点N处,MN与CD相交于点P,连接EP.设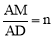 ,其中0<n≤1.
,其中0<n≤1.
(1)如图2,当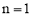 (即M点与D点重合),
(即M点与D点重合),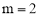 时,则
时,则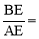 ;
;
(2)如图3,当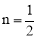 (M为AD的中点),m的值发生变化时,求证:
(M为AD的中点),m的值发生变化时,求证: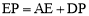 ;
;
(3)如图1,当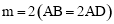 ,n的值发生变化时,
,n的值发生变化时,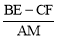 的值是否发生变化?说明理由.
的值是否发生变化?说明理由.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江西省九年级下学期第一次段考数学试卷(解析版) 题型:解答题
如图,抛物线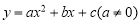 的图象过点C(0,1),顶点为Q(2,3)点D在x轴正半轴上,且线段OD=OC
的图象过点C(0,1),顶点为Q(2,3)点D在x轴正半轴上,且线段OD=OC
(1)求直线CD的解析式;
(2)求抛物线的解析式;
(3)将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E,求证:△CEQ∽△CDO;
(4)在(3)的条件下,若点P是线段QE上的动点,点F是线段OD上的动点,问:在P点和F点的移动过程中,△PCF的周长是否存在最小值?若存在,求出这个最小值,若不存在,请说明理由。

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江西省九年级下学期第一次段考数学试卷(解析版) 题型:填空题
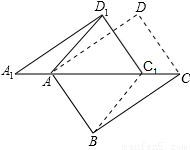
如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1、BC1。若∠ACB=30°,AB=1,CC1=x,△ACD与△A1C1D1重叠部分的面积为s,则下列结论:①△A1AD1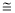 △CC1B;②当x=l时,四边形ABC1D1是菱形;③当x=2时,△BDD1为等边三角形;④
△CC1B;②当x=l时,四边形ABC1D1是菱形;③当x=2时,△BDD1为等边三角形;④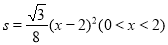 ;其中正确的是 (填序号)
;其中正确的是 (填序号)
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省苏州市高新区中考学二模数试卷(解析版) 题型:选择题
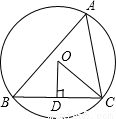
如图,△ABC内接于⊙O,OD⊥BC于D,∠A=50°,则∠OCD的度数是( )
A.40° B.45° C.50° D.60°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com