
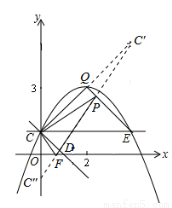
如图,抛物线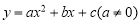 的图象过点C(0,1),顶点为Q(2,3)点D在x轴正半轴上,且线段OD=OC
的图象过点C(0,1),顶点为Q(2,3)点D在x轴正半轴上,且线段OD=OC
(1)求直线CD的解析式;
(2)求抛物线的解析式;
(3)将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E,求证:△CEQ∽△CDO;
(4)在(3)的条件下,若点P是线段QE上的动点,点F是线段OD上的动点,问:在P点和F点的移动过程中,△PCF的周长是否存在最小值?若存在,求出这个最小值,若不存在,请说明理由。

(1)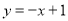 ;(2)y=
;(2)y=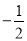 x2+2x+1; (3)证明见解析;(4)
x2+2x+1; (3)证明见解析;(4) .
.
【解析】
试题分析:(1)利用待定系数法求出直线解析式;
(2)利用待定系数法求出抛物线的解析式;
(3)关键是证明△CEQ与△CDO均为等腰直角三角形;
(4)如图所示,作点C关于直线QE的对称点C′,作点C关于x轴的对称点C″,连接C′C″,交OD于点F,交QE于点P,则△PCF即为符合题意的周长最小的三角形,由轴对称的性质可知,△PCF的周长等于线段C′C″的长度.利用轴对称的性质、两点之间线段最短可以证明此时△PCF的周长最小.如图③所示,利用勾股定理求出线段C′C″的长度,即△PCF周长的最小值.
(1)C(0,1),D(1,0)
∴直线CD的解析式为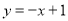 ;
;
(2)设抛物线解析式为y=a(x-2)2+3,
易得y=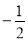 (x-2)2+3=
(x-2)2+3= x2+2x+1
x2+2x+1
(3)OC=OD,OC⊥OD,∴△OCD为等腰直角三角形,
对称轴x=2与CE交于点M,M(2,1)
易知△QMC与△QME是等腰直角三角形
∴△ CQE也是等腰直角三角形
∴△CEQ∽△CDO
(4)存在。
如图作点C关于直线QE的对称点C′,作点C关于x轴的对称点C″,连接C′C″,交OD于点F,交QE于点P,则△PCF即为符合题意的周长最小的三角形,由轴对称性得:
PC=PC′ CF=C″F
C,C′关于直线QE对称
C′(4,5)
又C″(-1,0) C′C″=
∴△PCF的周长最小值是
考点:二次函数综合题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2013-2014学年河北省邯郸市九年级中考二模数学试卷(解析版) 题型:填空题
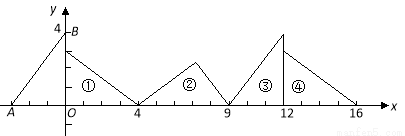
如图,在直角坐标系中,已知点 ,
, ,对 △
,对 △ 连续作旋转变换,依次得到三角形①、②、③、④…,则有一顶点坐标为(36,3)的三角形是 (填三角形的序号).
连续作旋转变换,依次得到三角形①、②、③、④…,则有一顶点坐标为(36,3)的三角形是 (填三角形的序号).
查看答案和解析>>
科目:初中数学 来源:2013-2014学年河北省保定市毕业生第一次模拟考试数学试卷(解析版) 题型:选择题
如果一个多边形的每个外角都等于36°,则这个多边形的边数是
A.4 B.6 C.8 D.10
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江西省九年级下学期期中模拟考试数学试卷(解析版) 题型:填空题
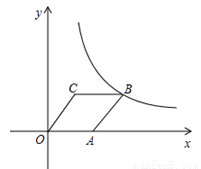
如图,菱形OABC的顶点C的坐标为(3,4).顶点A在x轴的正半轴上,反比例函数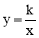 (x>0)的图象经过顶点B,则k的值为 .
(x>0)的图象经过顶点B,则k的值为 .
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江西省九年级下学期期中模拟考试数学试卷(解析版) 题型:选择题
如图,D为△ABC内一点,CD平分∠ACB,BE⊥CD,垂足为D,交AC于点E, .若
.若 ,
, ,则BD的长为( )
,则BD的长为( )

A、1 B、1.5 C、2 D、2.5
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江西省九年级下学期第一次段考数学试卷(解析版) 题型:解答题
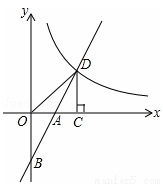
如图,在平面直角坐标系中,直线y=2x+b(b<0)与坐标轴交于A,B两点,与双曲线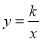 (x>0)交于D点,过点D作DC⊥x轴,垂足为C,连接OD。已知△AOB≌△ACD。
(x>0)交于D点,过点D作DC⊥x轴,垂足为C,连接OD。已知△AOB≌△ACD。
(1)如果b=-2,求k的值;
(2)试探究k与b的数量关系,并写出直线OD的解析式。
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江西省九年级下学期第一次段考数学试卷(解析版) 题型:填空题
已知二次函数y=-x2+2x+m的部分图象如图所示,则关于x的一元二次方程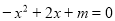 的解为 。
的解为 。

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省中考一模数学试卷(解析版) 题型:解答题
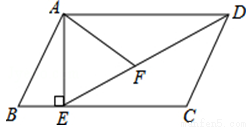
如图,在□ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6 ,AF=4
,AF=4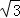 ,求AE的长.
,求AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com