解:(1)设所求的二次函数的解析式为y=ax
2+bx+c,∵抛物线经过A(4,-3),B(2,1)和C(-1,-8)三点,
∴
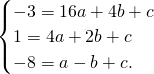
解之,得
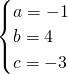
∴抛物线为y=-x
2+4x-3,令y=0,得-x
2+4x-3=0,解得x
1=1,x
2=3.
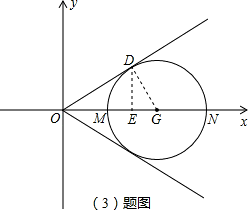
∴抛物线与x轴的交点坐标为M(1,0),N(3,0).
(2)过原点O作⊙G的切线,切点为D.易知OM=1,ON=3.由切割线定理,得OD
2=OM•ON=1×3.
∴OD=

,即所求的切线OD长为

.
(3)如右图,连接DG,则∠ODG=90°,DG=1.∵OG=2,∴∠DOG=30°.
过D作DE⊥OG,垂足为E,则DE=OD•sin30°=

,DE=OD•cos30°=

.
∴点D的坐标为D(

,

)或(

,-

).从而直线OD的解析式为y=±

x.
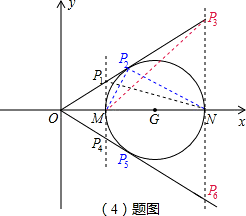
(4)Ⅰ、当点P在x轴上方时;
①点M是直角顶点,此时MP1⊥x轴,即M、P1的横坐标相同;
当x=1时,y=

x=

;
即 P
1(1,

);
②当点P是直角顶点时,由(2)知,P
2、D重合,即P
2(

,

);
③当点N是直角顶点,同①可求得 P
3(3,

).
Ⅱ、当点P在x轴下方时,同Ⅰ可知:P
4(1,-

),P
5(

,-

),P
6(3,-

).
综上,在直线OD上存在点P,使△MNP是直角三角形.所求P点的坐标为(1,±

),或(3,±

),或(

,±

).
分析:(1)已知函数图象上三个不同点的坐标,利用待定系数法即可求得抛物线的解析式;再令函数值为0,就能求出点M、N的坐标(注意它们的位置).
(2)在(1)题中,已经求得了M、N的坐标,则线段OM、ON的长可知,直接利用切割线定理即可求出OD的长.
(3)利用待定系数法求直线OD的解析式,必须先求出点D的坐标;连接圆心和切点,过点D作x轴的垂线OE(垂足为E),首先由半径长和OD的长求出∠DOG的度数,然后在Rt△ODE中,通过解直角三角形求出DE、OE的长,则点D的坐标可知,由此得解(需要注意的是:点D可能在x轴上方,也可能在x轴下方,所以直线OE的解析式应该有两个).
(4)在(3)中,已经知道共有两条直线OD,所以要分两种大的情况讨论,它们的解答方法是一致的,以点P在x轴上方为例进行说明:
①当点M是直角顶点时,MP所在直线与x轴垂直,即M、P的横坐标相同,直接将点M的横坐标代入直线OD的解析式中即可得到点P的坐标;
②当点P是直角顶点时,由圆周角定理知:(2)题的切点D正好符合点P的条件;
③当点N是直角顶点时,方法同①.
点评:此题是几何与代数知识的综合运用,在考查常规知识的同时,结合圆的对称性等渗透了分类讨论思想.解答(3)(4)问时,解题者常拘泥于习惯性思维,只考虑到在x轴上方的切线OD和以P为直角顶点的Rt△MNP这些常见情形,从而导致丢解.作为压轴题,本题(4)问显示出了层次性,由易到难,逐步深入,体现了命题者的匠心.

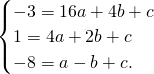 解之,得
解之,得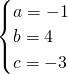
 ∴抛物线与x轴的交点坐标为M(1,0),N(3,0).
∴抛物线与x轴的交点坐标为M(1,0),N(3,0). ,即所求的切线OD长为
,即所求的切线OD长为 .
. ,DE=OD•cos30°=
,DE=OD•cos30°= .
. ,
, )或(
)或( ,-
,- ).从而直线OD的解析式为y=±
).从而直线OD的解析式为y=± x.
x. (4)Ⅰ、当点P在x轴上方时;
(4)Ⅰ、当点P在x轴上方时; x=
x= ;
; );
); ,
, );
); ).
). ),P5(
),P5( ,-
,- ),P6(3,-
),P6(3,- ).
). ),或(3,±
),或(3,± ),或(
),或( ,±
,± ).
).

 已知一个二次函数的图象经过A(0,1)、B(2,3)、C(-1,-
已知一个二次函数的图象经过A(0,1)、B(2,3)、C(-1,- (2012•嘉定区一模)已知一个二次函数的图象经过A(0,3)、B(4,3)、C(1,0)三点(如图).
(2012•嘉定区一模)已知一个二次函数的图象经过A(0,3)、B(4,3)、C(1,0)三点(如图).