
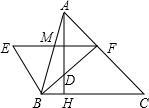
 如图,△ABC中,AH⊥BC,BF平分∠ABC,BE⊥BF,EF∥BC,以下四个结论:①∠E=∠ABE;②∠ADF-∠BAH=$\frac{1}{2}$∠ABC;③∠ADF=∠AFD;④S△ABF=$\frac{FM•AH}{2}$.其中正确的有( )
如图,△ABC中,AH⊥BC,BF平分∠ABC,BE⊥BF,EF∥BC,以下四个结论:①∠E=∠ABE;②∠ADF-∠BAH=$\frac{1}{2}$∠ABC;③∠ADF=∠AFD;④S△ABF=$\frac{FM•AH}{2}$.其中正确的有( )| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
分析 ①由BE⊥BF知∠1+∠ABE=90°,∠E+∠3=90°,EF∥BC知∠3=∠2,BF平分∠ABC,∠1=∠2,从而得到∠1=∠3,故∠E与∠ABE相等;
②由∠ADF=∠1+∠BAH,BF平分∠ABC,可得,∠1=∠2=$\frac{1}{2}$∠ABC,故∠ADF-∠BAH=$\frac{1}{2}$∠ABC正确;
③由∠ADF=∠BAH+∠1,∠AFD=∠3+∠AFM,由EF∥BC知∠3=∠2,BF平分∠ABC,∠1=∠2,又由∠BAH+∠DAF<90°,∠DAF+∠AFM=90°,则∠BAH<∠AFM,从而可得∠ADF<∠AFD;
④因为S△ABF=S△AMF+S△BMF,而以MF为底边,△AMF和△BMF的高之和等于AH,从而可得S△ABF=$\frac{FM•AH}{2}$正确.
解答 解:如图所示,∵BE⊥BF,
∴∠1+∠ABE=90°,∠E+∠3=90°.
又∵BF平分∠ABC,
∴∠1=∠2.
∵EF∥BC,
∴∠3=∠2.
∴∠1=∠3.
∴∠E=∠ABE.(故①正确)
∵∠ADF=∠1+∠BAH,
∴∠ADF-∠BAH=∠1.
又∵BF平分∠ABC,
∴∠1=∠2=∠ABC.
∴∠ADF-∠BAH=$\frac{1}{2}$∠ABC.(故②正确)
∵∠ADF=∠BAH+∠1,∠AFD=∠3+∠AFM,BF平分∠ABC,EF∥BC,
∴∠1=∠2=∠3.
又∵AH⊥BC,
∴∠BAH+∠DAF<90°,∠DAF+∠AFM=90°.
∴∠BAH<∠AFM.
即∠ADF<∠AFD.(故③错误)
∵S△ABF=S△AMF+S△BMF,设△AMF与△BMF以MF为底,底边上的高分别为h1,h2,
∴${S}_{△AMF}=\frac{MF×{h}_{1}}{2},{S}_{△BMF}=\frac{MF×{h}_{2}}{2}$.
∵h1+h2=AH,
∴${S}_{△AMF}=\frac{MF×AH}{2}$.(故④正确)
故选项A错误,选项B正确,选项C错误,选项D错误.
故选A.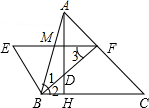
点评 此题主要考查了三角形的内角和定理,平行线的性质,角平分线的定义,三角形的外角和不相邻内角的关系,关键是根据题目中信息,灵活变化,判断结论是否正确,从而得到问题的答案.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
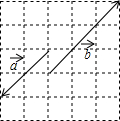 如图,由单位大小正方形拼成的5×5的大小正方形中,$\overrightarrow{a}$∥$\overrightarrow{b}$,求作:
如图,由单位大小正方形拼成的5×5的大小正方形中,$\overrightarrow{a}$∥$\overrightarrow{b}$,求作:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
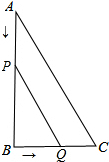 如图,在三角形ABC中,∠B=90°,AB=22cm,BC=20cm,点P从点A出发沿AB边向点B以2cm/s的速度移动,点Q从点B出发沿BC边向点C以1cm/s的速度移动,P、Q分别从A,B同时出发.
如图,在三角形ABC中,∠B=90°,AB=22cm,BC=20cm,点P从点A出发沿AB边向点B以2cm/s的速度移动,点Q从点B出发沿BC边向点C以1cm/s的速度移动,P、Q分别从A,B同时出发.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
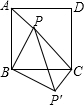 如图,将正方形ABCD中的△ABP绕点B顺时针旋转到△CBP′的位置,且BP=2,AP=1.
如图,将正方形ABCD中的△ABP绕点B顺时针旋转到△CBP′的位置,且BP=2,AP=1.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com