
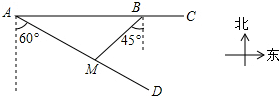
 某市对位于笔直公路AC上两个小区A、B的供水路线进行优化改造.供水站M在笔直公路AD上,测得供水站M在小区A的南偏东60°方向,在小区B的西南方向,小区A、B之间的距离为6米,求供水站M分别到小区A、B的距离.(结果保留根号)
某市对位于笔直公路AC上两个小区A、B的供水路线进行优化改造.供水站M在笔直公路AD上,测得供水站M在小区A的南偏东60°方向,在小区B的西南方向,小区A、B之间的距离为6米,求供水站M分别到小区A、B的距离.(结果保留根号) 分析 根据题意,在△ABM中,∠BAM=30°,∠ABM=45°,AB=6米.过点M作MN⊥AB于N,设MN=x米,用含x的代数式分别表示AN,BN,根据AN+BN=AB建立方程,解方程求出x的值,进而求出MA与MB的长.
解答 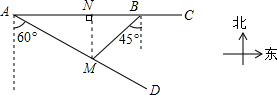 解:过点M作MN⊥AB于N,设MN=x米.
解:过点M作MN⊥AB于N,设MN=x米.
∵在Rt△AMN中,∠ANM=90°,∠MAN=30°,
∴MA=2MN=2x,AN=$\sqrt{3}$MN=$\sqrt{3}$x.
∵在Rt△AMN中,∠BNM=90°,∠MBN=45°,
∴BN=MN=x,MB=$\sqrt{2}$MN=$\sqrt{2}$x.
∵AN+BN=AB,
∴$\sqrt{3}$x+x=6,
∴x=3($\sqrt{3}$-1),
∴MA=2x=6$\sqrt{3}$-6,MB=$\sqrt{2}$x=3$\sqrt{6}$-3$\sqrt{2}$.
故供水站M到小区A的距离是(6$\sqrt{3}$-6)米,到小区B的距离是(3$\sqrt{6}$-3$\sqrt{2}$)米.
点评 本题考查了解直角三角形的应用-方向角问题,“化斜为直”是解三角形的基本思路,常需作垂线(高),原则上不破坏特殊角(30°、45°、60°).


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com