
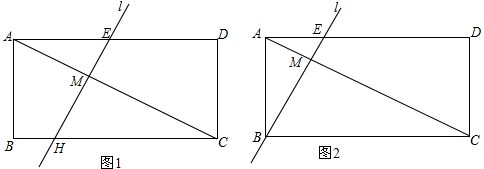
分析 (1)先根据勾股定理求出AC的长,再由锐角三角函数的定义得出∠BAC的度数,设l与AB交于点B′,根据直角三角形的性质可得出结论;
(2)设AE=x,则CH=3x,则x+DE=3x+BH,由S四边形BHEA:S四边形HCDE=2:7可得出DE=$\frac{13}{5}$x,BH=$\frac{3}{5}$x,AD=$\frac{18}{5}$x,过点M作MG⊥HC,则MG∥AB,在Rt△CMN中,MG⊥CH,由射影定理得得出x的值,进而得出结论;
(3)①根据l过点B时AD最长,过点D时AD最短即可得出结论;
②设AE=a,BC=x,过点M作MQ⊥BC于点Q,由(2)得,MQ=$\frac{3}{4}$,CQ=$\frac{3}{4}$x,HC=3a,HQ=3a-$\frac{3}{4}$x,由射影定理得,$\frac{3}{4}$x•(3a-$\frac{3}{4}$x)=$\frac{9}{16}$①,再根据AE∥BC可得出$\frac{a}{3a-x}$=$\frac{AG}{1-AG}$②,两式联立可得出a的值,进而得出结论.
解答 解:(1)∵四边形ABCD是矩形,
∴∠ABC=90°.
∵BC=AD=$\sqrt{3}$,AB=1,
∴AC=2,
∴tan∠BAC=$\frac{BC}{AB}$=$\sqrt{3}$,
∴∠BAC=60°.
∵AM=$\frac{1}{4}$AC=$\frac{1}{2}$,设l与AB交于点B′,则在Rt△AB′M中,∠AB′M=30°,
∴AB′=2AM=1=AB,
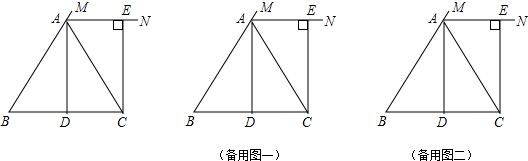
∴B′与B重合,即点B在直线l上;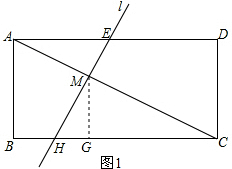 (2)如图1,∵AD∥BC,
(2)如图1,∵AD∥BC,
∴$\frac{AE}{CH}$=$\frac{AM}{MC}$=$\frac{1}{3}$.
设AE=x,则CH=3x,则x+DE=3x+BH①,
∵S四边形BHEA:S四边形HCDE=2:7,
∴$\frac{\frac{1}{2}(AE+BH)×1}{\frac{1}{2}(CH+DE)×1}$=$\frac{2}{7}$,即7BH+x=2DE②,
由①②得,DE=$\frac{13}{5}$x,BH=$\frac{3}{5}$x,AD=$\frac{18}{5}$x,
过点M作MG⊥HC,则MG∥AB,
∴$\frac{MG}{AB}$=$\frac{CM}{AC}$=$\frac{CG}{BC}$=$\frac{3}{4}$,
∴MG=$\frac{3}{4}$,CG=$\frac{27}{10}$x,CH=3x-$\frac{27}{10}$x=$\frac{3}{10}$x,
在Rt△CMN中,MG⊥CH,由射影定理得,MG2=HG•CG,即$\frac{9}{16}$=$\frac{3}{10}$x•$\frac{27}{10}$x,解得x=$\frac{5}{6}$,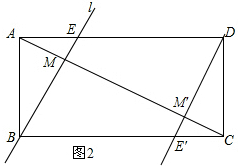
∴AD=$\frac{18}{5}$×$\frac{5}{6}$=3.
(3)①如图2,当l过点B时,由射影定理,AB2=AM•AC,即1=AM•4AM,可得AM=$\frac{1}{2}$,AC=4×$\frac{1}{2}$=2,AD=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$;
当l过点D时,由射影定理,CD2=AC•CM′,即1=4AM•3AM,可得AM′=$\sqrt{\frac{1}{12}}$=$\frac{\sqrt{3}}{6}$,AC=4×$\frac{\sqrt{3}}{6}$=$\frac{2\sqrt{3}}{3}$,AD=$\sqrt{{(\frac{2\sqrt{3}}{3})}^{2}-{1}^{2}}$=$\frac{\sqrt{3}}{3}$.
∴$\frac{\sqrt{3}}{3}$≤x≤$\sqrt{3}$.
②如图2,设AE=a,BC=x,过点M作MQ⊥BC于点Q,由(2)得,MQ=$\frac{3}{4}$,CQ=$\frac{3}{4}$x,HC=3a,HQ=3a-$\frac{3}{4}$x,
由射影定理得,$\frac{3}{4}$x•(3a-$\frac{3}{4}$x)=$\frac{9}{16}$,整理得,x2-4ax=1①,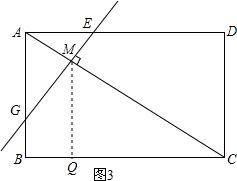
∵S矩形ABCD=AB•BC=x,
∴S△AGE=$\frac{1}{7}$x.
∵AE∥BC,
∴$\frac{AE}{BH}$=$\frac{AG}{BG}$,即$\frac{a}{3a-x}$=$\frac{AG}{1-AG}$,整理得AG=$\frac{a}{4a-x}$,
∴$\frac{1}{2}$×$\frac{a}{4a-x}$×a=$\frac{1}{7}$x,
∴7a2=8ax-2x2,
∴x2-4ax=-$\frac{7}{2}$a2②,
由①②得,$\frac{7}{2}$a2=1,解得a=$\frac{2\sqrt{7}}{7}$.
点评 本题考查的是四边形综合题,涉及到射影定理、矩形的性质及直角三角形的性质,根据题意作出辅助线,再利用射影定理求解是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
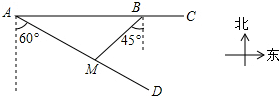 某市对位于笔直公路AC上两个小区A、B的供水路线进行优化改造.供水站M在笔直公路AD上,测得供水站M在小区A的南偏东60°方向,在小区B的西南方向,小区A、B之间的距离为6米,求供水站M分别到小区A、B的距离.(结果保留根号)
某市对位于笔直公路AC上两个小区A、B的供水路线进行优化改造.供水站M在笔直公路AD上,测得供水站M在小区A的南偏东60°方向,在小区B的西南方向,小区A、B之间的距离为6米,求供水站M分别到小区A、B的距离.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com