
分析 先将第二个方程转化为两个一次方程,可得:y=0或2y+x=0,原方程组化为两个方程组;再解这两个方程组即可解答.
解答 解:$\left\{\begin{array}{l}{{x}^{2}-{y}^{2}=12①}\\{y(2y+x)=0②}\end{array}\right.$
由②得,y=0或2y-x=0,
因此,原方程组化为两个方程组$\left\{\begin{array}{l}{{x}^{2}-{y}^{2}=0}\\{y=0}\end{array}\right.$,$\left\{\begin{array}{l}{{x}^{2}-{y}^{2}=0}\\{2y-x=0}\end{array}\right.$,
分别解这两个方程组,得原方程组的解为:$\left\{\begin{array}{l}{x=2\sqrt{3}}\\{y=0}\end{array}\right.$,$\left\{\begin{array}{l}{x=-2\sqrt{3}}\\{y=0}\end{array}\right.$,$\left\{\begin{array}{l}{x=-4}\\{y=2}\end{array}\right.$,$\left\{\begin{array}{l}{x=4}\\{y=-2}\end{array}\right.$.
点评 本题主要考查二元二次方程,解决高次方程的关键是将高次方程降次,将第二个方程转化为两个一次方程是解决此题的关键..


科目:初中数学 来源: 题型:选择题
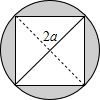 如图,直径为2a的圆中有一个正方形,那么阴影部分的面积为( )
如图,直径为2a的圆中有一个正方形,那么阴影部分的面积为( )| A. | (4-π)a2 | B. | (π-3)a2 | C. | (π-2.5)a2 | D. | (π-2)a2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
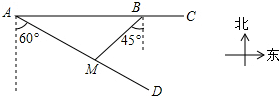 某市对位于笔直公路AC上两个小区A、B的供水路线进行优化改造.供水站M在笔直公路AD上,测得供水站M在小区A的南偏东60°方向,在小区B的西南方向,小区A、B之间的距离为6米,求供水站M分别到小区A、B的距离.(结果保留根号)
某市对位于笔直公路AC上两个小区A、B的供水路线进行优化改造.供水站M在笔直公路AD上,测得供水站M在小区A的南偏东60°方向,在小区B的西南方向,小区A、B之间的距离为6米,求供水站M分别到小区A、B的距离.(结果保留根号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com