
分析 先确定抛物线y=x2+2x的顶点坐标为(-1,-1)和抛物线y=x2+2x与x轴的交点为(-2,0),(0,0),画出抛物线,然后把抛物线y=x2+2x图象x轴下方的部分沿x轴翻折到x轴上方,则翻折部分的抛物线解析式为y=-(x+1)2+1(-2≤x≤0),有图象可得当直线y=$\frac{1}{2}$x+b过点A时,直线y=$\frac{1}{2}$x+b与该新图象恰好有三个公共点,易得对应的b的值为1;当直线y=$\frac{1}{2}$x+b与抛物线y=-(x+1)2+1(-2≤x≤0)相切时,直线y=$\frac{1}{2}$x+b与该新图象恰好有三个公共点,即-(x+1)2+1=$\frac{1}{2}$x+b有相等的实数解,利用根的判别式的意义可求出此时b的值.
解答 解:∵y=x2+2x=(x+1)2-1,
∴抛物线y=x2+2x的顶点坐标为(-1,-1),
当y=0时,x2+2x=0,解得x1=0,x2=-2,则抛物线y=x2+2x与x轴的交点为(-2,0),(0,0),
把抛物线y=x2+2x图象x轴下方的部分沿x轴翻折到x轴上方,则翻折部分的抛物线解析式为y=-(x+1)2+1(-2≤x≤0),
如图,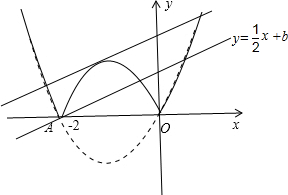
把直线y=$\frac{1}{2}$x向上平移,当平移后的直线y=$\frac{1}{2}$x+b过点A时,直线y=$\frac{1}{2}$x+b与该新图象恰好有三个公共点,所以$\frac{1}{2}$×(-2)+b=0,解得b=1;
当直线y=$\frac{1}{2}$x+b与抛物线y=-(x+1)2+1(-2≤x≤0)相切时,直线y=$\frac{1}{2}$x+b与该新图象恰好有三个公共点,即-(x+1)2+1=$\frac{1}{2}$x+b有相等的实数解,整理得x2+$\frac{5}{2}$x+b=0,△=($\frac{5}{2}$)2-4b=0,解得b=$\frac{25}{16}$,
所以b的值为1或$\frac{25}{16}$.
点评 本题考查了二次函数与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
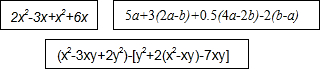
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
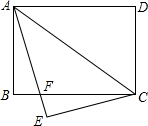 如图,矩形ABCD中,AB=6,BC=8,将△ACD沿对角线AC翻折得△ACE,AE交BC于点F,将△CEF绕点C逆时针旋转α角(0°<α<180°)得△CE′F′,点E、F的对应点分别为E、F的对应点分别为E′、F′.旋转过程中直线CF′、E′F′分别交直线AE于点M、N,当△F′NM是等腰三角形且MN=MF′时,则MN=$\frac{275}{56}$.
如图,矩形ABCD中,AB=6,BC=8,将△ACD沿对角线AC翻折得△ACE,AE交BC于点F,将△CEF绕点C逆时针旋转α角(0°<α<180°)得△CE′F′,点E、F的对应点分别为E、F的对应点分别为E′、F′.旋转过程中直线CF′、E′F′分别交直线AE于点M、N,当△F′NM是等腰三角形且MN=MF′时,则MN=$\frac{275}{56}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com