
【题目】如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5.OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C. 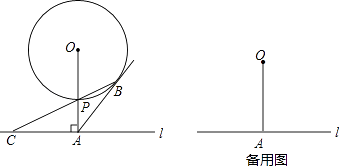
(1)试判断线段AB与AC的数量关系,并说明理由;
(2)若PC=2 ![]() ,求⊙O的半径和线段PB的长;
,求⊙O的半径和线段PB的长;
(3)若在⊙O上存在点Q,使△QAC是以AC为底边的等腰三角形,求⊙O的半径r的取值范围.
【答案】
(1)解:AB=AC,理由如下:
连接OB.
∵AB切⊙O于B,OA⊥AC,
∴∠OBA=∠OAC=90°,
∴∠OBP+∠ABP=90°,∠ACP+∠APC=90°,
∵OP=OB,
∴∠OBP=∠OPB,
∵∠OPB=∠APC,
∴∠ACP=∠ABC,
∴AB=AC;
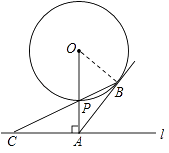
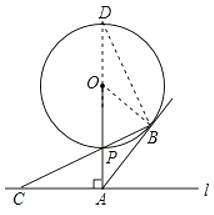
(2)解:延长AP交⊙O于D,连接BD,
设圆半径为r,则OP=OB=r,PA=5﹣r,
则AB2=OA2﹣OB2=52﹣r2,
AC2=PC2﹣PA2= ![]() ﹣(5﹣r)2,
﹣(5﹣r)2,
∴52﹣r2= ![]() ﹣(5﹣r)2,
﹣(5﹣r)2,
解得:r=3,
∴AB=AC=4,
∵PD是直径,
∴∠PBD=90°=∠PAC,
又∵∠DPB=∠CPA,
∴△DPB∽△CPA,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得:PB= ![]() .
.
∴⊙O的半径为3,线段PB的长为 ![]() ;
;
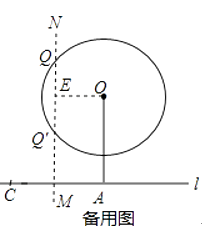
(3)解:作出线段AC的垂直平分线MN,作OE⊥MN,则可以推出OE= ![]() AC=
AC= ![]() AB=
AB= ![]()
又∵圆O与直线MN有交点,
∴OE= ![]() ≤r,
≤r,
![]() ≤2r,
≤2r,
25﹣r2≤4r2,
r2≥5,
∴r≥ ![]() ,
,
又∵圆O与直线相离,
∴r<5,
即 ![]() ≤r<5.
≤r<5.
【解析】(1)连接OB,根据切线的性质和垂直得出∠OBA=∠OAC=90°,推出∠OBP+∠ABP=90°,∠ACP+∠CPA=90°,求出∠ACP=∠ABC,根据等腰三角形的判定推出即可;(2)延长AP交⊙O于D,连接BD,设圆半径为r,则OP=OB=r,PA=5﹣r,根据AB=AC推出52﹣r2= ![]() ﹣(5﹣r)2,求出r,证△DPB∽△CPA,得出
﹣(5﹣r)2,求出r,证△DPB∽△CPA,得出 ![]() =
= ![]() ,代入求出即可;(3)根据已知得出Q在AC的垂直平分线上,作出线段AC的垂直平分线MN,作OE⊥MN,求出OE<r,求出r范围,再根据相离得出r<5,即可得出答案.
,代入求出即可;(3)根据已知得出Q在AC的垂直平分线上,作出线段AC的垂直平分线MN,作OE⊥MN,求出OE<r,求出r范围,再根据相离得出r<5,即可得出答案.
【考点精析】本题主要考查了等腰三角形的性质和勾股定理的概念的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角);直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,某校组织八年级1000名学生参加汉字听写大赛.为了解学生整体听写能力,从中抽取部分学生的成绩(得分取正整数,满分为100分)进行统计分析,请根据尚未完成的下列图表,解答下列问题:
组别 | 分数段 | 频数 | 频率 |
一 | 50.5~60.5 | 16 | 0.08 |
二 | 60.5~70.5 | 30 | 0.15 |
三 | 70.5~80.5 | m | 0.25 |
四 | 80.5~90.5 | 80 | n |
五 | 90.5~100.5 | 24 | 0.12 |
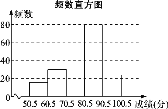
(1)写出表中:m,n,此样本中成绩的中位数落在第几组内;
(2)补全频数直方图;
(3)若成绩超过80分为优秀,该校八年级学生中汉字听写能力优秀的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明去爬山,在山脚看山顶角度为30°,小明在坡比为5:12的山坡上走1300米,此时小明看山顶的角度为60°,求山高( )
A.600﹣250 ![]() 米
米
B.600 ![]() ﹣250米
﹣250米
C.350+350 ![]() 米
米
D.500 ![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB=CD,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连接AF,CE,若DE=BF,则下列结论:①CF=AE;②OE=OF;③四边形ABCD是平行四边形;④图中共有四对全等三角形.其中正确结论的个数是

A.4 B.3 C.2 D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级四个班在植树节这天义务植树![]() 一班植树x棵,二班植树的棵数比一班的2倍少40棵,三班植树的棵数比二班的一半多30棵,四班植树的棵数比三班的三分之一多50棵.
一班植树x棵,二班植树的棵数比一班的2倍少40棵,三班植树的棵数比二班的一半多30棵,四班植树的棵数比三班的三分之一多50棵.
![]() 求这四个班共植树多少棵
求这四个班共植树多少棵![]() 用含x的代数式表示
用含x的代数式表示![]() ;
;
![]() 当
当![]() 时,四个班哪个班植树最多?
时,四个班哪个班植树最多?
![]() 若四个班共植树266棵,一班植树多少棵.
若四个班共植树266棵,一班植树多少棵.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
小明遇到一个问题:在![]() 中,
中,![]() ,
,![]() ,
,![]() 三边的长分别为
三边的长分别为![]() 、
、![]() 、
、![]() ,求
,求![]() 的面积.
的面积.
小明是这样解决问题的:如图①所示,先画一个正方形网格(每个小正方形的边长为![]() ),再在网格中画出格点
),再在网格中画出格点![]() (即
(即![]() 三个顶点都在小正方形的顶点处),从而借助网格就能计算出
三个顶点都在小正方形的顶点处),从而借助网格就能计算出![]() 的面积.他把这种解决问题的方法称为构图法.
的面积.他把这种解决问题的方法称为构图法.
参考小明解决问题的方法,完成下列问题:
(![]() )图
)图![]() 是一个
是一个![]() 的正方形网格(每个小正方形的边长为
的正方形网格(每个小正方形的边长为![]() ) .
) .
①利用构图法在答卷的图![]() 中画出三边长分别为
中画出三边长分别为![]() 、
、![]() 、
、![]() 的格点
的格点![]() .
.
②计算①中![]() 的面积为__________.(直接写出答案)
的面积为__________.(直接写出答案)
(![]() )如图
)如图![]() ,已知
,已知![]() ,以
,以![]() ,
,![]() 为边向外作正方形
为边向外作正方形![]() ,
,![]() ,连接
,连接![]() .
.
①判断![]() 与
与![]() 面积之间的关系,并说明理由.
面积之间的关系,并说明理由.
②若![]() ,
,![]() ,
,![]() ,直接写出六边形
,直接写出六边形![]() 的面积为__________.
的面积为__________.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将两个直角三角尺的顶点O叠放在一起

(1)如图(1)若∠BOD=35°,则∠AOC=___;若∠AOC=135°,则∠BOD=___;
(2)如图(2)若∠AOC=140°,则∠BOD=___;
(3)猜想∠AOC与∠BOD的大小关系,并结合图(1)说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列变形中:
①由方程![]() =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;
②由方程![]() x=
x=![]() 两边同除以
两边同除以![]() ,得x=1;
,得x=1;
③由方程6x﹣4=x+4移项,得7x=0;
④由方程2﹣![]() 两边同乘以6,得12﹣x﹣5=3(x+3).
两边同乘以6,得12﹣x﹣5=3(x+3).
错误变形的个数是( )个.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com