
【题目】将两个直角三角尺的顶点O叠放在一起

(1)如图(1)若∠BOD=35°,则∠AOC=___;若∠AOC=135°,则∠BOD=___;
(2)如图(2)若∠AOC=140°,则∠BOD=___;
(3)猜想∠AOC与∠BOD的大小关系,并结合图(1)说明理由.
【答案】(1)145°,45°;(2)40°;(3)∠AOC与∠BOD互补,理由见解析
【解析】
(1)由于是两直角三角形板重叠,根据∠AOC=∠AOB+∠COD-∠BOD可分别计算出∠AOC、∠BOD的度数;
(2)根据∠BOD=360°-∠AOC-∠AOB-∠COD计算可得;
(3)由∠AOD+∠BOD+∠BOD+∠BOC=180°且∠AOD+∠BOD+∠BOC=∠AOC可知两角互补;
解:(1)若∠BOD=35°,
∵∠AOB=∠COD=90°,
∴∠AOC=∠AOB+∠COD-∠BOD=90°+90°-35°=145°,
若∠AOC=135°,
则∠BOD=∠AOB+∠COD-∠AOC=90°+90°-135°=45°;
(2)如图2,若∠AOC=140°,
则∠BOD=360°-∠AOC-∠AOB-∠COD=40°;
(3)∠AOC与∠BOD互补,理由如下,
∵∠AOD+∠BOD+∠BOD+∠BOC=180°,
∵∠AOD+∠BOD+∠BOC=∠AOC,
∴∠AOC+∠BOD=180°,
即∠AOC与∠BOD互补.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中的两点A(m,0),B(2m,0)(m>0),二次函数y=ax2+bx+m的图象与x轴交与A,B两点与y轴交于点C,顶点为点D.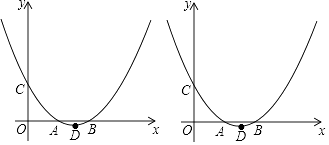
(1)当m=1时,直线BC的解析式为 , 二次函数y=ax2+bx+m的解析式为;
(2)求二次函数y=ax2+bx+m的解析式为(用含m的式子表示);
(3)连接AC、AD、BD,请你探究 ![]() 的值是否与m有关?若有关,求出它与m的关系;若无关,说明理由;
的值是否与m有关?若有关,求出它与m的关系;若无关,说明理由;
(4)当m为正整数时,依次得到点A1 , A2 , …,Am的横坐标分别为1,2,…m;点B1 , B2 , …,Bm 的横坐标分别为2,4,…2m(m≤10);经过点A1 , B1 , 点A2 , B2 , …,点Am , Bm的这组抛物线y=ax2+bx+m分别与y轴交于点C1 , C2 , …,Cm , 由此得到了一组直线B1C1 , B2C2 , …,BmCm , 在点B1 , B2 , …,Bm 中任取一点Bn , 以线段OBn为边向上作正方形OBnEnFn , 若点En在这组直线中的一条直线上,直接写出所有满足条件的点En的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5.OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C. 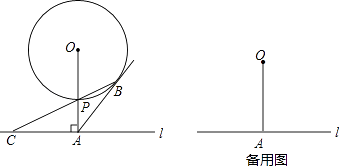
(1)试判断线段AB与AC的数量关系,并说明理由;
(2)若PC=2 ![]() ,求⊙O的半径和线段PB的长;
,求⊙O的半径和线段PB的长;
(3)若在⊙O上存在点Q,使△QAC是以AC为底边的等腰三角形,求⊙O的半径r的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
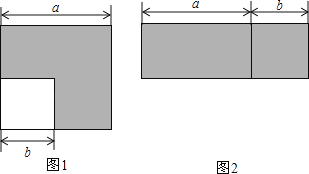
【题目】如图1所示,边长为a的正方形中有一个边长为b的小正方形,如图2所示是由图1中阴影部分拼成的一个正方形.
(1)设图1中阴影部分面积为S1,图2中阴影部分面积为S2.请直接用含a,b的代数式表示S1,S2;
(2)请写出上述过程所揭示的乘法公式;
(3)试利用这个公式计算:(2+1)(22+1)(24+1)(28+1)+1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,给出了下列三个论断:①对角线AC平分∠BAD;②CD=BC;③∠D+∠B=180°.在上述三个论断中,若以其中两个论断作为条件,另外一个论断作为结论,则可以得出______个正确的命题.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF. 
(1)求证:△ABF≌△CBE;
(2)判断△CEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC,CD⊥AB于D点,M,N是AC,BC上的动点,且∠MDN=90°,下列结论:①AM=CN;②四边形MDNC的面积为定值;③AM2+BN2=MN2;④NM平分∠CND.其中正确的是 ( )

A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润y1与投资量x成正比例关系,种植花卉的利润y2与投资量x的平方成正比例关系,并得到了表格中的数据.
投资量x(万元) | 2 |
种植树木利润y1(万元) | 4 |
种植花卉利润y2(万元) | 2 |
(1)分别求出利润y1与y2关于投资量x的函数关系式;
(2)如果这位专业户以8万元资金投入种植花卉和树木,设他投入种植花卉金额m万元,种植花卉和树木共获利利润W万元,直接写出W关于m的函数关系式,并求他至少获得多少利润?他能获取的最大利润是多少?
(3)若该专业户想获利不低于22万,在(2)的条件下,直接写出投资种植花卉的金额m的范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com