
【题目】如图,点E正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF. 
(1)求证:△ABF≌△CBE;
(2)判断△CEF的形状,并说明理由.
【答案】
(1)证明:∵四边形ABCD是正方形,
∴AB=CB,∠ABC=90°,
∵△EBF是等腰直角三角形,其中∠EBF=90°,
∴BE=BF,
∴∠ABC﹣∠CBF=∠EBF﹣∠CBF,
∴∠ABF=∠CBE.
在△ABF和△CBE中,有  ,
,
∴△ABF≌△CBE(SAS).

(2)解:△CEF是直角三角形.理由如下:
∵△EBF是等腰直角三角形,
∴∠BFE=∠FEB=45°,
∴∠AFB=180°﹣∠BFE=135°,
又∵△ABF≌△CBE,
∴∠CEB=∠AFB=135°,
∴∠CEF=∠CEB﹣∠FEB=135°﹣45°=90°,
∴△CEF是直角三角形.
【解析】(1)由四边形ABCD是正方形可得出AB=CB,∠ABC=90°,再由△EBF是等腰直角三角形可得出BE=BF,通过角的计算可得出∠ABF=∠CBE,利用全等三角形的判定定理SAS即可证出△ABF≌△CBE;(2)根据△EBF是等腰直角三角形可得出∠BFE=∠FEB,通过角的计算可得出∠AFB=135°,再根据全等三角形的性质可得出∠CEB=∠AFB=135°,通过角的计算即可得出∠CEF=90°,从而得出△CEF是直角三角形.


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,某校组织八年级1000名学生参加汉字听写大赛.为了解学生整体听写能力,从中抽取部分学生的成绩(得分取正整数,满分为100分)进行统计分析,请根据尚未完成的下列图表,解答下列问题:
组别 | 分数段 | 频数 | 频率 |
一 | 50.5~60.5 | 16 | 0.08 |
二 | 60.5~70.5 | 30 | 0.15 |
三 | 70.5~80.5 | m | 0.25 |
四 | 80.5~90.5 | 80 | n |
五 | 90.5~100.5 | 24 | 0.12 |
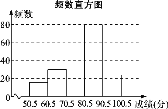
(1)写出表中:m,n,此样本中成绩的中位数落在第几组内;
(2)补全频数直方图;
(3)若成绩超过80分为优秀,该校八年级学生中汉字听写能力优秀的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
小明遇到一个问题:在![]() 中,
中,![]() ,
,![]() ,
,![]() 三边的长分别为
三边的长分别为![]() 、
、![]() 、
、![]() ,求
,求![]() 的面积.
的面积.
小明是这样解决问题的:如图①所示,先画一个正方形网格(每个小正方形的边长为![]() ),再在网格中画出格点
),再在网格中画出格点![]() (即
(即![]() 三个顶点都在小正方形的顶点处),从而借助网格就能计算出
三个顶点都在小正方形的顶点处),从而借助网格就能计算出![]() 的面积.他把这种解决问题的方法称为构图法.
的面积.他把这种解决问题的方法称为构图法.
参考小明解决问题的方法,完成下列问题:
(![]() )图
)图![]() 是一个
是一个![]() 的正方形网格(每个小正方形的边长为
的正方形网格(每个小正方形的边长为![]() ) .
) .
①利用构图法在答卷的图![]() 中画出三边长分别为
中画出三边长分别为![]() 、
、![]() 、
、![]() 的格点
的格点![]() .
.
②计算①中![]() 的面积为__________.(直接写出答案)
的面积为__________.(直接写出答案)
(![]() )如图
)如图![]() ,已知
,已知![]() ,以
,以![]() ,
,![]() 为边向外作正方形
为边向外作正方形![]() ,
,![]() ,连接
,连接![]() .
.
①判断![]() 与
与![]() 面积之间的关系,并说明理由.
面积之间的关系,并说明理由.
②若![]() ,
,![]() ,
,![]() ,直接写出六边形
,直接写出六边形![]() 的面积为__________.
的面积为__________.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将两个直角三角尺的顶点O叠放在一起

(1)如图(1)若∠BOD=35°,则∠AOC=___;若∠AOC=135°,则∠BOD=___;
(2)如图(2)若∠AOC=140°,则∠BOD=___;
(3)猜想∠AOC与∠BOD的大小关系,并结合图(1)说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将每件进价为80元的某种商品原来按每件100元出售,一天可售出100件.后来经过市场调查,发现这种商品单价每降低1元,其销量可增加10件.
(1)求商场经营该商品原来一天可获利润多少元?
(2)设后来该商品每件降价x元,商场一天可获利润y元.
①若商场经营该商品一天要获利润2160元,则每件商品应降价多少元?
②求出y与x之间的函数关系式,并直接写出当x取何值时,商场获利润不少于2160元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:等腰三角形OAB在直角坐标系中的位置如下图,点A的坐标为( ![]() ,3),点B的坐标为(﹣6,0).
,3),点B的坐标为(﹣6,0). 
(1)若△OAB关于y轴的轴对称图形是△OA'B',请直接写出A、B的对称点A'、B'的坐标;
(2)若将△OAB沿x轴向右平移a个单位,此时点A恰好落在反比例函数 ![]() 的图象上,求a的值;
的图象上,求a的值;
(3)若△OAB绕点O按逆时针方向旋转30°,此时点B恰好落在反比例函数 ![]() 的图象上,求k的值.
的图象上,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某沿海开放城市A接到台风警报,在该市正南方向100km的B处有一台风中心,沿BC方向以20km/h的速度向D移动,已知城市A到BC的距离AD=60km,那么台风中心经过多长时间从B点移到D点?如果在距台风中心30km的圆形区域内都将有受到台风的破坏的危险,正在D点休闲的游人在接到台风警报后的几小时内撤离才可脱离危险?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列变形中:
①由方程![]() =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;
②由方程![]() x=
x=![]() 两边同除以
两边同除以![]() ,得x=1;
,得x=1;
③由方程6x﹣4=x+4移项,得7x=0;
④由方程2﹣![]() 两边同乘以6,得12﹣x﹣5=3(x+3).
两边同乘以6,得12﹣x﹣5=3(x+3).
错误变形的个数是( )个.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OM⊥AB.
(1)∠AOC的邻补角为 (写出一个即可);
(2)若∠1=∠2,判断ON与CD的位置关系,并说明理由;
(3)若∠1=![]() ∠BOC,求∠MOD的度数.
∠BOC,求∠MOD的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com