
【题目】如图![]() ,在直角边分别为
,在直角边分别为![]() 和
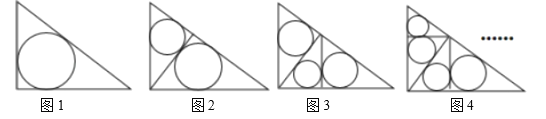
和![]() 的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,依此类推,图10中有
的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,依此类推,图10中有![]() 个直角三角形的内切圆,它们的面积分别记为
个直角三角形的内切圆,它们的面积分别记为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ________.
________.
科目:初中数学 来源: 题型:
【题目】为满足市场需求,某超市在五月初五“端午节”来临前夕,购进一种品牌粽子,每盒进价是40元.超市规定每盒售价不得少于45元.根据以往销售经验发现;当售价定为每盒45元时,每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)试求出每天的销售量y(盒)与每盒售价x(元)之间的函数关系式;
(2)当每盒售价定为多少元时,每天销售的利润P(元)最大?最大利润是多少?
(3)为稳定物价,有关管理部门限定:这种粽子的每盒售价不得高于58元.如果超市想要每天获得不低于6000元的利润,那么超市每天至少销售粽子多少盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=BC,BD⊥AC于点D,∠FAC=![]() ∠ABC,且∠FAC在AC下方.点P,Q分别是射线BD,射线AF上的动点,且点P不与点B重合,点Q不与点A重合,连接CQ,过点P作PE⊥CQ于点E,连接DE.
∠ABC,且∠FAC在AC下方.点P,Q分别是射线BD,射线AF上的动点,且点P不与点B重合,点Q不与点A重合,连接CQ,过点P作PE⊥CQ于点E,连接DE.
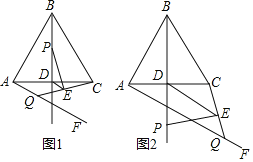
(1)若∠ABC=60°,BP=AQ.
①如图1,当点P在线段BD上运动时,请直接写出线段DE和线段AQ的数量关系和位置关系;
②如图2,当点P运动到线段BD的延长线上时,试判断①中的结论是否成立,并说明理由;
(2)若∠ABC=2α≠60°,请直接写出当线段BP和线段AQ满足什么数量关系时,能使(1)中①的结论仍然成立(用含α的三角函数表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,函数y=![]() (x>0)的图象G经过点A(4,1),与直线y=
(x>0)的图象G经过点A(4,1),与直线y=![]() x+b的图象交于点B,与y轴交于点C.其中横、纵坐标都是整数的点叫做整点.记图象G在点A、B之间的部分与线段OA、OC、BC围成的区域(不含边界)为W.若W内恰有4个整点,结合函数图象,b的取值范围是( )
x+b的图象交于点B,与y轴交于点C.其中横、纵坐标都是整数的点叫做整点.记图象G在点A、B之间的部分与线段OA、OC、BC围成的区域(不含边界)为W.若W内恰有4个整点,结合函数图象,b的取值范围是( )
A.﹣![]() ≤b<1或
≤b<1或![]() <b≤
<b≤![]() B.﹣
B.﹣![]() ≤b<1或
≤b<1或![]() <b≤
<b≤![]()
C.﹣![]() ≤b<﹣1或﹣
≤b<﹣1或﹣![]() <b≤
<b≤![]() D.﹣
D.﹣![]() ≤b<﹣1或
≤b<﹣1或![]() <b≤
<b≤![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=BC,∠ABC=90°,D为AC中点,点P是线段AD上的一点,点P与点A、点D不重合),连接BP.将△ABP绕点P按顺时针方向旋转α角(0°<α<180°),得到△A1B1P,连接A1B1、BB1
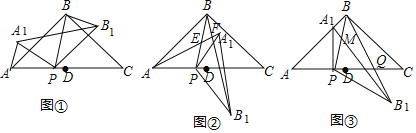
(1)如图①,当0°<α<90°,在α角变化过程中,请证明∠PAA1=∠PBB1.
(2)如图②,直线AA1与直线PB、直线BB1分别交于点E,F.设∠ABP=β,当90°<α<180°时,在α角变化过程中,是否存在△BEF与△AEP全等?若存在,求出α与β之间的数量关系;若不存在,请说明理由;
(3)如图③,当α=90°时,点E、F与点B重合.直线A1B与直线PB相交于点M,直线BB′与AC相交于点Q.若AB=![]() ,设AP=x,CQ=y,求y关于x的函数关系式.
,设AP=x,CQ=y,求y关于x的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆有50个房间供游客居住,当每个房间定价120元时,房间会全部住满,当每个房间每天的定价每增加10元时,就会有一个房间空闲。如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用,设每个房间定价增加10 x元(x为整数)。
(1)(2分)直接写出每天游客居住的房间数量y与x的函数关系式。
(2)(4分)设宾馆每天的利润为W元,当每间房价定价为多少元时,宾馆每天所获利润最大,最大利润是多少?
(3)(4分)某日,宾馆了解当天的住宿的情况,得到以下信息:①当日所获利润不低于5000元,②宾馆为游客居住的房间共支出费用没有超过600元,③每个房间刚好住满2人。问:这天宾馆入住的游客人数最少有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 经过点
经过点![]() ,与y轴交于点B,与抛物线
,与y轴交于点B,与抛物线![]() 的对称轴交于点
的对称轴交于点![]() .
.
(1)求m的值;
(2)求抛物线的顶点坐标;
(3)![]() 是线段AB上一动点,过点N作垂直于y轴的直线与抛物线交于点
是线段AB上一动点,过点N作垂直于y轴的直线与抛物线交于点![]() ,
,![]() (点P在点Q的左侧).若
(点P在点Q的左侧).若![]() 恒成立,结合函数的图象,求a的取值范围.
恒成立,结合函数的图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前我市“校园手机”现象越来越受到社会关注,针对这种现象,我市某中学九年级数学兴趣小组的同学随机调查了学校若干名家长对“中学生带手机”现象的看法.统计整理并制作了如下的统计图:
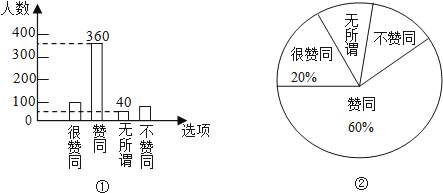
(1)这次调查的家长总数为__________,家长表示“不赞同”的人数为________________;
(2)从这次接受调查的家长中随机抽查一个,恰好是“赞同”的家长的概率是____________;
(3)求图②中表示家长“无所谓”的扇形圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴交于
轴交于![]() 两点
两点
![]() 求抛物线
求抛物线![]() 的解析式;
的解析式;
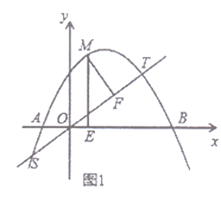
![]() 如图1,直线
如图1,直线![]() 交抛物线
交抛物线![]() 于
于![]() 两点,
两点,![]() 为抛物线
为抛物线![]() 上
上![]() 之间的动点,过
之间的动点,过![]() 点作
点作![]() 轴于点
轴于点![]() 于点
于点![]() ,求
,求![]() 的最大值;
的最大值;
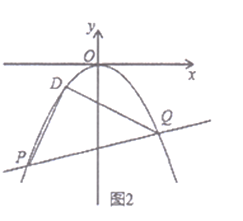
![]() 如图2,平移抛物线
如图2,平移抛物线![]() 的顶点到原点得抛物线
的顶点到原点得抛物线![]() ,直线
,直线![]() 交抛物线
交抛物线![]() 于
于![]() 、
、![]() 两点,在抛物线
两点,在抛物线![]() 上存在一个定点
上存在一个定点![]() ,使
,使![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com