
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 经过点
经过点![]() ,与y轴交于点B,与抛物线
,与y轴交于点B,与抛物线![]() 的对称轴交于点
的对称轴交于点![]() .
.
(1)求m的值;
(2)求抛物线的顶点坐标;
(3)![]() 是线段AB上一动点,过点N作垂直于y轴的直线与抛物线交于点
是线段AB上一动点,过点N作垂直于y轴的直线与抛物线交于点![]() ,
,![]() (点P在点Q的左侧).若
(点P在点Q的左侧).若![]() 恒成立,结合函数的图象,求a的取值范围.
恒成立,结合函数的图象,求a的取值范围.
 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】初中数学代数知识中,方程、函数、不等式存在着紧密的联系,请阅读下列两则材料,回答问题:
利用函数图象找方程![]() 解的范围.设函数
解的范围.设函数![]() ,当
,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .则函数
.则函数![]() 的图象经过两个点
的图象经过两个点![]() 与
与![]() ,而点
,而点![]() 在
在![]() 轴下方,点
轴下方,点![]() 在
在![]() 轴上方,则该函数图象与
轴上方,则该函数图象与![]() 轴交点横坐标必大于-2,小于-1.故,方程
轴交点横坐标必大于-2,小于-1.故,方程![]() 的有解,且该解的范围为
的有解,且该解的范围为![]() .
.
材料二:
解一元二次不等式![]() .由“异号两数相乘,结果为负可得:
.由“异号两数相乘,结果为负可得:
情况①![]() ,得
,得![]() ,则
,则![]()
情况②![]() ,得
,得![]() ,则无解
,则无解
故,![]() 的解集为
的解集为![]() .
.
(1)请根据材料一解决问题:已知方程![]() 有唯一解
有唯一解![]() ,且
,且![]() (
(![]() 为整数),求整数
为整数),求整数![]() 的值.
的值.
(2)请结合材料一与材料二解决问题:若关于![]() 的方程
的方程![]() 的解分别为
的解分别为![]() ,
,![]() ,且
,且![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某防洪指挥部发现长江边一处长500米,高10米,背水坡的坡角为45°的防洪大堤(横断面为梯形ABCD)急需加固.经调查论证,防洪指挥部专家组制定的加固方案是:背水坡面用土石进行加固,并使上底加宽3米,加固后背水坡EF的坡比i=1:![]() .
.
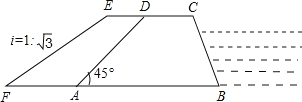
(1)求加固后坝底增加的宽度AF;
(2)求完成这项工程需要土石多少立方米.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
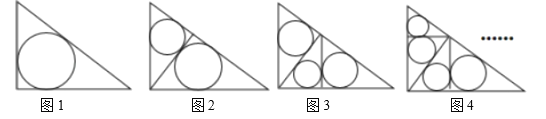
【题目】如图![]() ,在直角边分别为
,在直角边分别为![]() 和
和![]() 的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,依此类推,图10中有
的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,依此类推,图10中有![]() 个直角三角形的内切圆,它们的面积分别记为
个直角三角形的内切圆,它们的面积分别记为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ________.
________.
查看答案和解析>>
科目:初中数学 来源: 题型:
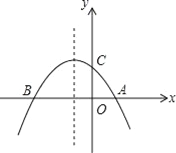
【题目】如图,已知抛物线y=﹣![]() x2﹣
x2﹣![]() x+2与x轴交于A、B两点,与y轴交于点C
x+2与x轴交于A、B两点,与y轴交于点C
(1)求点A,B,C的坐标;
(2)点E是此抛物线上的点,点F是其对称轴上的点,求以A,B,E,F为顶点的平行四边形的面积;
(3)此抛物线的对称轴上是否存在点M,使得△ACM是等腰三角形?若存在,请求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
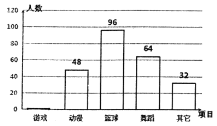
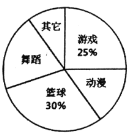
【题目】某地区对学生业余爱好进行抽样调查,被抽取的同学每人在下面五项:“游戏”,“动漫”,“篮球”,“舞蹈”“其它”中选一项最喜欢的活动,并将调查结果绘制成以下两幅不完整的统计图,请根据图中的信息,解答下列问题:
(1)这次抽样调查中,一共抽查了多少名学生?
(2)请补全条形统计图;
(3)根据调查结果,估计该地区5000名学生中有多少人最喜欢“舞蹈”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“六一”儿童节前夕,某部队战士到福利院慰问儿童.战士们从营地出发,匀速步行前往文具店选购礼物,停留一段时间后,继续按原速步行到达福利院(营地、文具店、福利院三地依次在同一直线上).到达后因接到紧急任务,立即按原路匀速跑步返回营地(赠送礼物的时间忽略不计),下列图象能大致反映战
士们离营地的距离![]() 与时间
与时间![]() 之间函数关系的是( )
之间函数关系的是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一根长为![]() 的铁丝剪成两段,并把每一段铁丝围成一个正方形.若设围成的一个正方形的边长为
的铁丝剪成两段,并把每一段铁丝围成一个正方形.若设围成的一个正方形的边长为![]() .
.
(1)要使这两个正方形的面积的和等于![]() ,则剪出的两段铁丝长分别是多少?
,则剪出的两段铁丝长分别是多少?
(2)剪出的两段铁丝长分别是多少![]() 时,这两个正方形的面积和最小?最小值是多少?
时,这两个正方形的面积和最小?最小值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com