
【题目】如图,某防洪指挥部发现长江边一处长500米,高10米,背水坡的坡角为45°的防洪大堤(横断面为梯形ABCD)急需加固.经调查论证,防洪指挥部专家组制定的加固方案是:背水坡面用土石进行加固,并使上底加宽3米,加固后背水坡EF的坡比i=1:![]() .
.
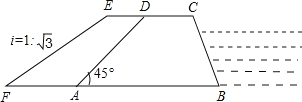
(1)求加固后坝底增加的宽度AF;
(2)求完成这项工程需要土石多少立方米.(结果保留根号)
【答案】(1)(10![]() ﹣7)米;(2)(25000
﹣7)米;(2)(25000![]() ﹣10000)立方米.
﹣10000)立方米.
【解析】
(1)分别过E、D作AB的垂线,设垂足为G、H.在Rt△EFG中,根据坡面的铅直高度(即坝高)及坡比,即可求出水平宽FG的长;同理可在Rt△ADH中求出AH的长;由AF=FG+GH﹣AH求出AF的长.
(2)已知了梯形AFED的上下底和高,易求得其面积.梯形AFED的面积乘以坝长即为所需的土石的体积.
解:(1)分别过点E、D作EG⊥AB、DH⊥AB交AB于G、H.
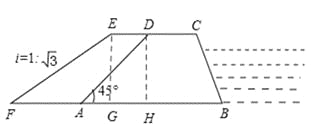
∵四边形ABCD是梯形,且AB∥CD,
∴DH![]() EG.
EG.
∴四边形EGHD是矩形.∴ED=GH.
在Rt△ADH中,
AH=DH÷tan∠DAH=10÷tan45°=10(米),
在Rt△FGE中,![]() ,
,
∴FG=![]() EG=10
EG=10![]() (米).
(米).
∴AF=FG+GH﹣AH=10![]() +3﹣10=10
+3﹣10=10![]() ﹣7(米).
﹣7(米).
答:加固后坝底增加的宽度AF为(10![]() ﹣7)米.
﹣7)米.
(2)加宽部分的体积V=S梯形AFED×坝长=![]() ×(3+10
×(3+10![]() ﹣7)×10×500=25000
﹣7)×10×500=25000![]() 10000(立方米).
10000(立方米).
答:完成这项工程需要土石(25000![]() ﹣10000)立方米.
﹣10000)立方米.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
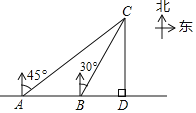
【题目】今年“五一”期间,小明一家到某农庄采摘,在村口A处,小明接到农庄发来的定位,发现农庄C在自己的北偏东45°方向,于是沿河边笔直绿道l步行200米到达B处,此时定位显示农庄C在自己的北偏东30°方向,电话联系,得知农庄主已到农庄C正南方的桥头D处等待,请问还要沿绿道直走多少米才能到达桥头D处.(精确到1米,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
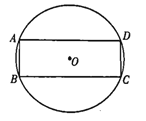
【题目】如图,⊙O为短形ABCD的外接圆,其半径为3.
(1)用尺规作图作出∠ABC的平分线,并标出它与劣弧AD的交点E(保留作图痕迹,不写作法);
(2)若(1)中的点E到弦AD的距离为2,求弦AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=BC,BD⊥AC于点D,∠FAC=![]() ∠ABC,且∠FAC在AC下方.点P,Q分别是射线BD,射线AF上的动点,且点P不与点B重合,点Q不与点A重合,连接CQ,过点P作PE⊥CQ于点E,连接DE.
∠ABC,且∠FAC在AC下方.点P,Q分别是射线BD,射线AF上的动点,且点P不与点B重合,点Q不与点A重合,连接CQ,过点P作PE⊥CQ于点E,连接DE.
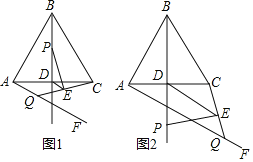
(1)若∠ABC=60°,BP=AQ.
①如图1,当点P在线段BD上运动时,请直接写出线段DE和线段AQ的数量关系和位置关系;
②如图2,当点P运动到线段BD的延长线上时,试判断①中的结论是否成立,并说明理由;
(2)若∠ABC=2α≠60°,请直接写出当线段BP和线段AQ满足什么数量关系时,能使(1)中①的结论仍然成立(用含α的三角函数表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中直线y=x﹣2与y轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2).

(1)求反比例函数的关系式;
(2)将直线y=x﹣2向上平移后与反比例函数图象在第一象限内交于点C,且△ABC的面积为18,求平移后的直线的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,函数y=![]() (x>0)的图象G经过点A(4,1),与直线y=
(x>0)的图象G经过点A(4,1),与直线y=![]() x+b的图象交于点B,与y轴交于点C.其中横、纵坐标都是整数的点叫做整点.记图象G在点A、B之间的部分与线段OA、OC、BC围成的区域(不含边界)为W.若W内恰有4个整点,结合函数图象,b的取值范围是( )
x+b的图象交于点B,与y轴交于点C.其中横、纵坐标都是整数的点叫做整点.记图象G在点A、B之间的部分与线段OA、OC、BC围成的区域(不含边界)为W.若W内恰有4个整点,结合函数图象,b的取值范围是( )
A.﹣![]() ≤b<1或
≤b<1或![]() <b≤
<b≤![]() B.﹣
B.﹣![]() ≤b<1或
≤b<1或![]() <b≤
<b≤![]()
C.﹣![]() ≤b<﹣1或﹣
≤b<﹣1或﹣![]() <b≤
<b≤![]() D.﹣
D.﹣![]() ≤b<﹣1或
≤b<﹣1或![]() <b≤
<b≤![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
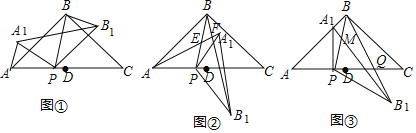
【题目】在△ABC中,AB=BC,∠ABC=90°,D为AC中点,点P是线段AD上的一点,点P与点A、点D不重合),连接BP.将△ABP绕点P按顺时针方向旋转α角(0°<α<180°),得到△A1B1P,连接A1B1、BB1
(1)如图①,当0°<α<90°,在α角变化过程中,请证明∠PAA1=∠PBB1.
(2)如图②,直线AA1与直线PB、直线BB1分别交于点E,F.设∠ABP=β,当90°<α<180°时,在α角变化过程中,是否存在△BEF与△AEP全等?若存在,求出α与β之间的数量关系;若不存在,请说明理由;
(3)如图③,当α=90°时,点E、F与点B重合.直线A1B与直线PB相交于点M,直线BB′与AC相交于点Q.若AB=![]() ,设AP=x,CQ=y,求y关于x的函数关系式.
,设AP=x,CQ=y,求y关于x的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 经过点
经过点![]() ,与y轴交于点B,与抛物线
,与y轴交于点B,与抛物线![]() 的对称轴交于点
的对称轴交于点![]() .
.
(1)求m的值;
(2)求抛物线的顶点坐标;
(3)![]() 是线段AB上一动点,过点N作垂直于y轴的直线与抛物线交于点
是线段AB上一动点,过点N作垂直于y轴的直线与抛物线交于点![]() ,
,![]() (点P在点Q的左侧).若
(点P在点Q的左侧).若![]() 恒成立,结合函数的图象,求a的取值范围.
恒成立,结合函数的图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 在抛物线
在抛物线![]() 上,且该抛物线与
上,且该抛物线与![]() 轴分别交于点
轴分别交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
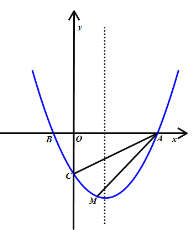
(1)求抛物线的解析式及对称轴;
(2)若点![]() 是抛物线对称轴上的一个动点,求
是抛物线对称轴上的一个动点,求![]() 的最小值;
的最小值;
(3)点![]() 是是抛物线上除点
是是抛物线上除点![]() 外的一点,若
外的一点,若![]() 与
与![]() 的面积相等,求点
的面积相等,求点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com