
【题目】如图,在平面直角坐标系中直线y=x﹣2与y轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2).

(1)求反比例函数的关系式;
(2)将直线y=x﹣2向上平移后与反比例函数图象在第一象限内交于点C,且△ABC的面积为18,求平移后的直线的函数关系式.
【答案】解:(1)将B坐标代入直线y=x﹣2中得:m﹣2=2,解得:m=4,
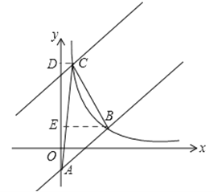
∴B(4,2),即BE=4,OE=2。
设反比例解析式为![]() ,
,
将B(4,2)代入反比例解析式得:k=8,
∴反比例解析式为![]() 。
。
(2)设平移后直线解析式为y=x+b,C(a,a+b),
对于直线y=x﹣2,令x=0求出y=﹣2,得到OA=2,
过C作CD⊥y轴,过B作BE⊥y轴,
将C坐标代入反比例解析式得:a(a+b)=8①,
∵![]() ,
,
∴![]() ②。
②。
①②联立,解得:b=7。
∴平移后直线解析式为y=x+7。
【解析】(1)设反比例解析式为![]() ,将B坐标代入直线y=x﹣2中求出m的值,确定出B坐标,将B坐标代入反比例解析式中求出k的值,即可确定出反比例解析式。
,将B坐标代入直线y=x﹣2中求出m的值,确定出B坐标,将B坐标代入反比例解析式中求出k的值,即可确定出反比例解析式。
(2)过C作CD垂直于y轴,过B作BE垂直于y轴,设y=x﹣2平移后解析式为y=x+b,C坐标为(a,a+b),由![]() ,根据已知三角形ABC面积列出关系式,将C坐标代入反比例解析式中列出关系式,两关系式联立求出b的值,即可确定出平移后直线的解析式。
,根据已知三角形ABC面积列出关系式,将C坐标代入反比例解析式中列出关系式,两关系式联立求出b的值,即可确定出平移后直线的解析式。


科目:初中数学 来源: 题型:
【题目】如图,点P为定角∠AOB的平分线上的一个定点,且∠MPN与∠AOB互补,若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:(1)PM=PN恒成立;(2)OM+ON的值不变;(3)四边形PMON的面积不变;(4)MN的长不变,其中正确的个数为( )

A. 4B. 3C. 2D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为开展体育大课间活动,某学校需要购买篮球与足球若干个,已知购买3个篮球和2个足球需求共需要575元,购买4个篮球和3个足球共需要785元.
![]() 购买一个篮球,一个足球各需多少元?
购买一个篮球,一个足球各需多少元?
![]() 若体育老师带了8000元去购买这种篮球与足球共80个,由于数量较多,店主给出篮球与足球一律打八折的优惠价,那么他最多能购买多少个篮球?同时买了多少个足球?
若体育老师带了8000元去购买这种篮球与足球共80个,由于数量较多,店主给出篮球与足球一律打八折的优惠价,那么他最多能购买多少个篮球?同时买了多少个足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,已知A(2,2)、B(﹣2,0)、C(﹣1,﹣2).

(1)在平面直角坐标系中画出△ABC;
(2)若点D与点C关于y轴对称,则点D的坐标为 ;
(3)求△ABC的面积;
(4)已知点P为x轴上一点,若S△ABP=5时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.

(1)求证:△ABE≌△CBF;
(2)若∠CAE=30°,求∠ACF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为提升硬件设施,决定采购80台电脑,现有A,B两种型号的电脑可供选择.已知每台A型电脑比B型的贵2000元,2台A型电脑与3台B型电脑共需24000元.
(1)分别求A,B两种型号电脑的单价;
(2)若A,B两种型号电脑的采购总价不高于38万元,则A型电脑最多采购多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,AC=6cm,BC=8cm,AB=10cm,CD为AB边上的高.动点P从点A出发,沿着△ABC的三条边逆时针走一圈回到A点,速度为2cm/s,设运动时间为t s.
(1)求CD的长;
(2)t为何值时,△ACP是等腰三角形?
(3)若M为BC上一动点,N为AB上一动点,是否存在M,N使得AM+MN 的值最小?如果有,请直接写出最小值,如果没有,请说明理由。



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】陈杰骑自行车去上学,当他以往常的速度骑了一段路时,忽然想起要买某本书,于是又折回到刚经过的一家书店,买到书后继续赶去学校.以下是他本次上学的路程与所用时间的关系示意图.根据图中提供的信息回答下列问题:
(1)陈杰家到学校的距离是多少米?书店到学校的距离是多少米?
(2)陈杰在书店停留了多少分钟?本次上学途中,陈杰一共行驶了多少米?
(3)在整个上学的途中哪个时间段陈杰骑车速度最快?最快的速度是多少米?
(4)如果陈杰不买书,以往常的速度去学校,需要多少分钟?本次上学比往常多用多少分钟?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com