
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.

(1)求证:△ABE≌△CBF;
(2)若∠CAE=30°,求∠ACF的度数.
【答案】(1)证明见解析;(2)60°.
【解析】
试题分析:(1)由∠ABC=90°就可以求出∠CBF=90°,由SAS就可以得出△ABE≌△CBF;
(2)由∠CAE=30°就可以求出∠BAE=15°,就可以得出∠BCF=15°,由条件可以求出∠ACB=45°,进而可以求出∠ACF的度数.
试题解析:(1)证明:∵∠ABC=90°,
∴∠ABC=∠CBF=90°.
在△ABE和△CBF中,
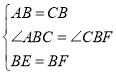 ,
,
∴△ABE≌△CBF(SAS);
(2)∵△ABE≌△CBF,
∴∠BAE=∠BCF.
∵∠ABC=90°,AB=CB,
∴∠BCA=∠BAC=45°.
∵∠CAE=30°,
∴∠BAE=15°,
∴∠BCF=15°.
∵∠ACF=∠BCF+∠ACB,
∴∠ACF=15°+45°=60°.
答:∠ACF的度数为60°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列说法中正确的有()
(1) 钝角的补角一定是锐角
(2) 过己知直线外一点作这条直线的垂线有且只有一条
(3) —个角的两个邻补角是对顶角
(4) 等角的补角相等
(5) 直线![]() 外一点A与直线
外一点A与直线![]() 上各点连接而成的所有线段中,最短线段的长是3cm,则
上各点连接而成的所有线段中,最短线段的长是3cm,则
点A到直线![]() 的距离是3cm .
的距离是3cm .
A. 2个 B. 3个 C. 4 个 D. 5 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于实数![]() 、
、![]() 我们定义一种新运算
我们定义一种新运算![]() (其中
(其中![]() 、
、![]() 均为非零常数).等式右边是通常的四则运算.由这种运算得到的数我们称之为线性数,记为
均为非零常数).等式右边是通常的四则运算.由这种运算得到的数我们称之为线性数,记为![]() ,其中
,其中![]() 、
、![]() 叫做线性数的一个数对.若实数
叫做线性数的一个数对.若实数![]() 、
、![]() 都取正整数,我们称这样的线性数为正格线性数,这时的
都取正整数,我们称这样的线性数为正格线性数,这时的![]() 、
、![]() 叫做正格线性数的正格数对.
叫做正格线性数的正格数对.
(1)若![]() ,则
,则![]()
![]() .
.
(2)已知![]() ,若正格线性数
,若正格线性数![]() ,求满足不等式组
,求满足不等式组![]() 的所有
的所有![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3.
(1)观察每次变换前后的三角形的变化规律,若将△OA3B3变换成△OA4B4,则A4的坐标是__,B4的坐标是__;
(2)若按第(1)题找到的规律将△OAB进行n次变换,得到△OAnBn,比较每次变换中三角形顶点坐标有何变化,找出规律,推测An的坐标是__,Bn的坐标是__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,A点坐标为(2,4),B点坐标为(﹣3,﹣2),C点坐标为(3,1).

(1)在图中画出△ABC关于y轴对称的△A′B′C′(不写画法),并写出点A′,B′,C′的坐标;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学将组织七年级学生春游一天,由王老师和甲、乙两同学到客车租赁公司洽谈租车事宜.
(1)两同学向公司经理了解租车的价格,公司经理对他们说:“公司有45座和60座两种型号的客车可供租用,60座的客车每辆每天的租金比45座的贵100元.”王老师说:“我们学校八年级昨天在这个公司租了5辆45座和2辆60座的客车,一天的租金为1600元,你们能知道45座和60座的客车每辆每天的租金各是多少元吗”甲、乙两同学想了一下,都说知道了价格.
聪明的你知道45座和60座的客车每辆每天的租金各是多少元吗?
(2)公司经理问:“你们准备怎样租车”,甲同学说:“我的方案是只租用45座的客车,可是会有一辆客车空出30个座位”;乙同学说“我的方案只租用60座客车,正好坐满且比甲同学的方案少用两辆客车”,王老师在﹣旁听了他们的谈话说:“从经济角度考虑,还有别的方案吗”?如果是你,你该如何设计租车方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系上有点A(1.O),点A第一次跳动至点A1(-1,1).第四次向右跳动5个单位至点A4(3,2),…,依此规律跳动下去,点A第100次跳动至点A100的坐标是( )

A. (50,49) B. (51, 49) C. (50, 50) D. (51, 50)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着纪录片《穹顶之下》的播出,全社会对空气污染问题越来越重视,空气净化器的销量也逐步增大.某商场从厂家购进了A,B两种型号的空气净化器,已知一台A型空气净化器的进价比一台B型空气净化器的进价多300元,用7 500元购进A型空气净化器和用6 000元购进B型空气净化器的台数相同.
(1)求一台A型空气净化器和一台B型空气净化器的进价各为多少元?
(2)经市场调查,当B型空气净化器的售价为1800元时,每天可卖出4台,在此基础上,售价每降低50元,每天将多售出1台,如果每天商场销售B型空气净化器的利润为3200元,请问该商场应将B型空气净化器的售价定为多少元?
(3)已知A型空气净化器净化能力为340m3/h,B型空气净化器净化能力为240m3/h.某公司室内办公场地总面积为600m2 , 室内墙高3.5m.受二胎政策影响,近期孕妇数量激增,为保证胎儿健康成长,该公司计划购买15台空气净化器净化空气,每天花费30分钟将室内空气净化一新,若不考虑空气对流等因素,该公司至少要购买A型空气净化器多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
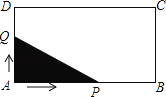
【题目】如图,长方形ABCD中,AB=8,AD=4.点Q与点P同时从点A出发,点Q以每秒1个单位的速度沿A→D→C→B的方向运动,点P以每秒3个单位的速度沿A→B→C→D的方向运动,当P,Q两点相遇时,它们同时停止运动.设Q点运动的时间为x(秒),在整个运动过程中,当△APQ为直角三角形时,则相应的x的值或取值范围是_______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com