
【题目】如图,△ABC中,A点坐标为(2,4),B点坐标为(﹣3,﹣2),C点坐标为(3,1).

(1)在图中画出△ABC关于y轴对称的△A′B′C′(不写画法),并写出点A′,B′,C′的坐标;
(2)求△ABC的面积.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,点C是线段AB上一点,△ACD和△BCE都是等边三角形,连结AE,BD,设AE交CD于点F.
(1)求证:△ACE≌△DCB;
(2)求证:△ADF∽△BAD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠MON=α,点P是∠MON角平分线上一点,点A在射线OM上,作∠APB=180°-α,交直线ON于点B,PC⊥ON于C.
(1)如图1,若∠MON=90°时,求证:PA=PB;
(2)如图2,若∠MON=60°时,写出线段OB,OA及BC之间的数量关系,并说明理由;
(3)如图3,若∠MON=60°时,点B在射线ON的反向延长线上时,(2)中结论还成立吗?若不成立,直接写出线段OB,OA及BC之间的数量关系(不需要证明).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年5月的第二周为:“职业教育活动周”,今年我市展开了以“弘扬工匠精神,打造技能强国”为主题的系列活动,活动期间某职业中学组织全校师生并邀请学生家长和社区居民参加“职教体验观摩”活动,相关职业技术人员进行了现场演示,活动后该校随机抽取了部分学生进行调查:“你最感兴趣的一种职业技能是什么?”并对此进行了统计,绘制了统计图(均不完整). 
(1)补全条形统计图和扇形统计图;
(2)若该校共有3000名学生,请估计该校对“工艺设计”最感兴趣的学生有多少人?
(3)要从这些被调查的学生中随机抽取一人进行访谈,那么正好抽到对“机电维修”最感兴趣的学生的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】双胞胎兄弟小明和小亮在同一班读书,某天放学后,小明和同学走路回家,途中没有停留,小亮骑车回家,他们各自与学校的距离S(米)与用去的时间t(分钟)的关系如图所示.根据图象提供的有关信息,下列说法中错误的是( )

A. 兄弟俩的家离学校1000米 B. 小亮中间停留了一段时间后,再以80米/分钟的速度骑回家
C. 他们同时到家,用时30分钟 D. 小明的速度为50米/分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.

(1)求证:△ABE≌△CBF;
(2)若∠CAE=30°,求∠ACF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,分别以点A和B为圆心,以相同的长(大于 ![]() AB)为半径作弧,两弧相交于点M和N,作直线MN交AB于点D,交BC于点E,连接CD,下列结论错误的是( )
AB)为半径作弧,两弧相交于点M和N,作直线MN交AB于点D,交BC于点E,连接CD,下列结论错误的是( ) 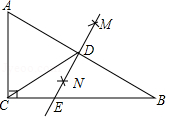
A.AD=BD
B.BD=CD
C.∠A=∠BED
D.∠ECD=∠EDC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,AB∥CD,分别探究下列四个图形(图①、②、③、④)中∠APC和∠PAB、∠PCD的数量关系,用等式表示出来.

(1)设∠APC=m,∠PAB=n,∠PCD=t.
请用含m,n,t的等式表示四个图形中相应的∠APC和∠PAB、∠PCD的数量关系.(直接写出结果)
图①: ;
图②: ;
图③: ;
图④: .
(2)在(1)中的4个结论中选出一个你喜欢的结论加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,以点A为圆心,AC的长为半径作 ![]() 交AB于点E,以点B为圆心,BC的长为半径作
交AB于点E,以点B为圆心,BC的长为半径作 ![]() 交AB于点D,则阴影部分的面积为 .
交AB于点D,则阴影部分的面积为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com