
【题目】如图,在△ABC中,∠ACB=90°,分别以点A和B为圆心,以相同的长(大于 ![]() AB)为半径作弧,两弧相交于点M和N,作直线MN交AB于点D,交BC于点E,连接CD,下列结论错误的是( )
AB)为半径作弧,两弧相交于点M和N,作直线MN交AB于点D,交BC于点E,连接CD,下列结论错误的是( ) 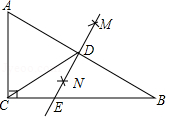
A.AD=BD
B.BD=CD
C.∠A=∠BED
D.∠ECD=∠EDC
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=9,AC=6,BC=12,点M在AB边上,且AM=3,过点M作直线MN与AC边交于点N,使截得的三角形与原三角形相似,则MN=__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙、丙三种糖果混合而成的什锦糖100千克,其中各种糖果的单价和千克数如表所示,商家用加权平均数来确定什锦糖的单价.
甲种糖果 | 乙种糖果 | 丙种糖果 | |
单价(元/千克) | 20 | 25 | 30 |
千克数 | 40 | 40 | 20 |
(1)求该什锦糖的单价.
(2)为了使什锦糖的单价每千克至少降低2元,商家计划在什锦糖中加入甲、丙两种糖果共100千克,问其中最多可加入丙种糖果多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,A点坐标为(2,4),B点坐标为(﹣3,﹣2),C点坐标为(3,1).

(1)在图中画出△ABC关于y轴对称的△A′B′C′(不写画法),并写出点A′,B′,C′的坐标;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)探究:如图①,直线AB、BC、AC两两相交,交点分别为点A、B、C,点D在线段AB上,过点D作DE∥BC交AC于点E,过点E作EF∥AB交BC于点F.若∠ABC=40°,求∠DEF的度数.
请将下面的解答过程补充完整,并填空(理由或数学式)
解:∵DE∥BC,∴∠DEF= .( )
∵EF∥AB,∴ =∠ABC.( )
∴∠DEF=∠ABC.(等量代换)
∵∠ABC=40°,∴∠DEF= °.
(2)应用:如图②,直线AB、BC、AC两两相交,交点分别为点A、B、C,点D在线段AB的延长线上,过点D作DE∥BC交AC于点E,过点E作EF∥AB交BC于点F.若∠ABC=60°,则∠DEF= °.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系上有点A(1.O),点A第一次跳动至点A1(-1,1).第四次向右跳动5个单位至点A4(3,2),…,依此规律跳动下去,点A第100次跳动至点A100的坐标是( )

A. (50,49) B. (51, 49) C. (50, 50) D. (51, 50)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
我们知道![]() 的几何意义是在数轴上数
的几何意义是在数轴上数![]() 对应的点与原点的距离,即
对应的点与原点的距离,即![]() =
=![]() ,也就是说,
,也就是说,![]() 表示在数轴上数
表示在数轴上数![]() 与数0对应的点之间的距离;这个结论可以推广为
与数0对应的点之间的距离;这个结论可以推广为![]() 表示在数轴上数
表示在数轴上数![]() 与数
与数![]() 对应的点之间的距离;
对应的点之间的距离;
例1.解方程|![]() |=2.因为在数轴上到原点的距离为2的点对应的数为
|=2.因为在数轴上到原点的距离为2的点对应的数为![]() ,所以方程|
,所以方程|![]() |=2的解为
|=2的解为![]() .
.
例2.解不等式|![]() -1|>2.在数轴上找出|
-1|>2.在数轴上找出|![]() -1|=2的解(如图),因为在数轴上到1对应的点的距离等于2的点对应的数为-1或3,所以方程|
-1|=2的解(如图),因为在数轴上到1对应的点的距离等于2的点对应的数为-1或3,所以方程|![]() -1|=2的解为
-1|=2的解为![]() =-1或
=-1或![]() =3,因此不等式|
=3,因此不等式|![]() -1|>2的解集为
-1|>2的解集为![]() <-1或
<-1或![]() >3.
>3.
![]()
例3.解方程|![]() -1|+|
-1|+|![]() +2|=5.由绝对值的几何意义知,该方程就是求在数轴上到1和-2对应的点的距离之和等于5的点对应的
+2|=5.由绝对值的几何意义知,该方程就是求在数轴上到1和-2对应的点的距离之和等于5的点对应的![]() 的值.因为在数轴上1和-2对应的点的距离为3(如图),满足方程的
的值.因为在数轴上1和-2对应的点的距离为3(如图),满足方程的![]() 对应的点在1的右边或-2的左边.若
对应的点在1的右边或-2的左边.若![]() 对应的点在1的右边,可得
对应的点在1的右边,可得![]() =2;若
=2;若![]() 对应的点在-2的左边,可得
对应的点在-2的左边,可得![]() =-3,因此方程|
=-3,因此方程|![]() -1|+|
-1|+|![]() +2|=5的解是
+2|=5的解是![]() =2或
=2或![]() =-3.
=-3.
![]()
参考阅读材料,解答下列问题:
(1)方程|![]() +3|=4的解为 ;
+3|=4的解为 ;
(2)解不等式:|![]() -3|≥5;
-3|≥5;
(3)解不等式:|![]() -3|+|
-3|+|![]() +4|≥9
+4|≥9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com