
【题目】正方形ABCD的边长是4,点P是AD边的中点,点E是正方形边上的一点.若△PBE是等腰三角形,则腰长为 .
【答案】2 ![]() ,或
,或 ![]() ,或
,或 ![]()
【解析】解:分情况讨论:(1)当PB为腰时,若P为顶点,则E点与C点重合,如图所示: 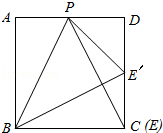
∵四边形ABCD是正方形,
∴AB=BC=CD=AD=4,∠A=∠C=∠D=90°,
∵P是AD的中点,
∴AP=DP=2,
根据勾股定理得:BP= ![]() =
= ![]() =2
=2 ![]() ;
;
若B为顶点,则根据PB=BE′得,E′为CD中点,此时腰长PB=2 ![]() ;(2)当PB为底边时,E在BP的垂直平分线上,与正方形的边交于两点,即为点E;①当E在AB上时,如图2所示:
;(2)当PB为底边时,E在BP的垂直平分线上,与正方形的边交于两点,即为点E;①当E在AB上时,如图2所示: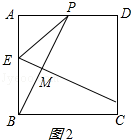
则BM= ![]() BP=
BP= ![]() ,
,
∵∠BME=∠A=90°,∠MBE=∠ABP,
∴△BME∽△BAP,
∴ ![]() ,即
,即 ![]() ,
,
∴BE= ![]() ;②当E在CD上时,如图3所示:
;②当E在CD上时,如图3所示: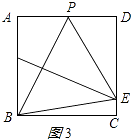
设CE=x,则DE=4﹣x,
根据勾股定理得:BE2=BC2+CE2 , PE2=DP2+DE2 ,
∴42+x2=22+(4﹣x)2 ,
解得:x= ![]() ,
,
∴CE= ![]() ,
,
∴BE= ![]() =
= ![]() =
= ![]() ;
;
综上所述:腰长为:2 ![]() ,或
,或 ![]() ,或
,或 ![]() ;
;
故答案为:2 ![]() ,或
,或 ![]() ,或
,或 ![]() .
.
分情况讨论:(1)当PB为腰时,若P为顶点,则E点和C点重合,求出PB长度即可;若B为顶点,则E点为CD中点;(2)当PB为底时,E在BP的垂直平分线上,与正方形的边交于两点,即为点E;①由题意得出BM= ![]() BP=
BP= ![]() ,证明△BME∽△BAP,得出比例式
,证明△BME∽△BAP,得出比例式 ![]() ,即可求出BE;②设CE=x,则DE=4﹣x,根据勾股定理得出方程求出CE,再由勾股定理求出BE即可.
,即可求出BE;②设CE=x,则DE=4﹣x,根据勾股定理得出方程求出CE,再由勾股定理求出BE即可.


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:初中数学 来源: 题型:
【题目】已知:∠MON=α,点P是∠MON角平分线上一点,点A在射线OM上,作∠APB=180°-α,交直线ON于点B,PC⊥ON于C.
(1)如图1,若∠MON=90°时,求证:PA=PB;
(2)如图2,若∠MON=60°时,写出线段OB,OA及BC之间的数量关系,并说明理由;
(3)如图3,若∠MON=60°时,点B在射线ON的反向延长线上时,(2)中结论还成立吗?若不成立,直接写出线段OB,OA及BC之间的数量关系(不需要证明).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,分别以点A和B为圆心,以相同的长(大于 ![]() AB)为半径作弧,两弧相交于点M和N,作直线MN交AB于点D,交BC于点E,连接CD,下列结论错误的是( )
AB)为半径作弧,两弧相交于点M和N,作直线MN交AB于点D,交BC于点E,连接CD,下列结论错误的是( ) 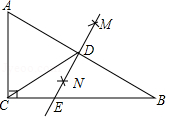
A.AD=BD
B.BD=CD
C.∠A=∠BED
D.∠ECD=∠EDC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,AB∥CD,分别探究下列四个图形(图①、②、③、④)中∠APC和∠PAB、∠PCD的数量关系,用等式表示出来.

(1)设∠APC=m,∠PAB=n,∠PCD=t.
请用含m,n,t的等式表示四个图形中相应的∠APC和∠PAB、∠PCD的数量关系.(直接写出结果)
图①: ;
图②: ;
图③: ;
图④: .
(2)在(1)中的4个结论中选出一个你喜欢的结论加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究题
(1)探究发现:
下面是一道例题及其解答过程,请补充完整:
如图①在等边△ABC内部,有一点P,若∠APB=150°.求证:AP2+BP2=CP2
证明:将△APC绕A点逆时针旋转60°,得到△AP′B,连接PP′,则△APP′为等边三角形
∴∠APP′=60° PA=PP′PC=
∵∠APB=150°∴∠BPP′=90°
∴P′P2+BP2=
即PA2+PB2=PC2
(2)类比延伸:
如图②在等腰三角形ABC中,∠BAC=90°,内部有一点P,若∠APB=135°,试判断线段PA、PB、PC之间的数量关系,并证明.
(3)联想拓展:
如图③在△ABC中,∠BAC=120°,AB=AC,点P在直线AB上方,且∠APB=60°,满足(kPA)2+PB2=PC2 , 请直接写出k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线L:y=﹣![]() x+2与x轴、y轴分别交于A、B两点,在y轴上有一点N(0,4),动点M从A点以每秒1个单位的速度匀速沿x轴向左移动.
x+2与x轴、y轴分别交于A、B两点,在y轴上有一点N(0,4),动点M从A点以每秒1个单位的速度匀速沿x轴向左移动.
(1)点A的坐标:_____;点B的坐标:_____;
(2)求△NOM的面积S与M的移动时间t之间的函数关系式;
(3)在y轴右边,当t为何值时,△NOM≌△AOB,求出此时点M的坐标;
(4)在(3)的条件下,若点G是线段ON上一点,连结MG,△MGN沿MG折叠,点N恰好落在x轴上的点H处,求点G的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年共享单车横空出世,更好地解决了人们“最后一公里”出行难的问题,截止到2016年底,已知“摩拜单车”投放数量有50万辆,“ofo共享单车”的投放数量是“摩拜单车”投放数量的1.6倍,“ofo共享单车”注册用户量比“摩拜单车”的注册用户量多210万人,据统计使用一辆“ofo共享单车”的平均人数比使用一辆“摩拜单车”的平均人数少3人,假设注册这两种单车的用户都在使用共享单车,求2016年“ofo共享单车”和“摩拜单车”的注册用户量各多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,以点A为圆心,AC的长为半径作 ![]() 交AB于点E,以点B为圆心,BC的长为半径作
交AB于点E,以点B为圆心,BC的长为半径作 ![]() 交AB于点D,则阴影部分的面积为 .
交AB于点D,则阴影部分的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蔬菜加工公司先后两批次收购蒜薹(tái)共100吨.第一批蒜薹价格为4000元/吨;因蒜薹大量上市,第二批价格跌至1000元/吨.这两批蒜薹共用去16万元.
(1)求两批次购进蒜薹各多少吨;
(2)公司收购后对蒜薹进行加工,分为粗加工和精加工两种:粗加工每吨利润400元,精加工每吨利润1000元.要求精加工数量不多于粗加工数量的三倍.为获得最大利润,精加工数量应为多少吨?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com