
【题目】(题文)如图,直线AB,CD相交于点O,OE⊥CD于点O,OD平分∠BOF,∠BOE=50![]() ,
,
求∠AOC,∠AOF,∠EOF的度数.

【答案】∠AOC=40 °,∠AOF=100 °,∠EOF=130°
【解析】根据题意即可推出∠EOD=90°,∠BOD=40°,既而得,∠AOC=40°,∠BOF=80°,得:∠EOF=130°,∠AOF=100°.
∵OE⊥CD于点O,
∴∠EOD=90°(垂直的定义) ,
∵∠BOE=50°,
∴∠BOD=90°-50°=40°,
∴∠AOC=∠BOD=40°(对顶角相等),
∵OD平分∠BOF,
∴∠BOF=2∠BOD=80°(角平分线的定义),
∴∠AOF=180°-80°=100°,(平角的定义).
∴∠EOF=∠EOB+∠BOF=130°.
答:∠AOC=40 °,∠AOF=100 °,∠EOF=130°.
点精:本题考查了垂线,角平分线的定义,对顶角、邻补角.


科目:初中数学 来源: 题型:
【题目】二次函数![]() 的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为(
的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为(![]() ,﹣2);⑤当x<
,﹣2);⑤当x<![]() 时,y随x的增大而减小;⑥a+b+c>0正确的有( )
时,y随x的增大而减小;⑥a+b+c>0正确的有( )

A. 3个 B. 4个 C. 5个 D. 6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】双胞胎兄弟小明和小亮在同一班读书,某天放学后,小明和同学走路回家,途中没有停留,小亮骑车回家,他们各自与学校的距离S(米)与用去的时间t(分钟)的关系如图所示.根据图象提供的有关信息,下列说法中错误的是( )

A. 兄弟俩的家离学校1000米 B. 小亮中间停留了一段时间后,再以80米/分钟的速度骑回家
C. 他们同时到家,用时30分钟 D. 小明的速度为50米/分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,分别以点A和B为圆心,以相同的长(大于 ![]() AB)为半径作弧,两弧相交于点M和N,作直线MN交AB于点D,交BC于点E,连接CD,下列结论错误的是( )
AB)为半径作弧,两弧相交于点M和N,作直线MN交AB于点D,交BC于点E,连接CD,下列结论错误的是( ) 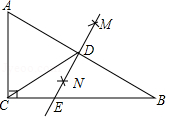
A.AD=BD
B.BD=CD
C.∠A=∠BED
D.∠ECD=∠EDC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的面积为36cm2 , 点E在BC上,点G在AB的延长线上,四边形EFGB是正方形,以点B为圆心,BC的长为半径画 ![]() ,连接AF,CF,则图中阴影部分的面积为 .
,连接AF,CF,则图中阴影部分的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,AB∥CD,分别探究下列四个图形(图①、②、③、④)中∠APC和∠PAB、∠PCD的数量关系,用等式表示出来.

(1)设∠APC=m,∠PAB=n,∠PCD=t.
请用含m,n,t的等式表示四个图形中相应的∠APC和∠PAB、∠PCD的数量关系.(直接写出结果)
图①: ;
图②: ;
图③: ;
图④: .
(2)在(1)中的4个结论中选出一个你喜欢的结论加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究题
(1)探究发现:
下面是一道例题及其解答过程,请补充完整:
如图①在等边△ABC内部,有一点P,若∠APB=150°.求证:AP2+BP2=CP2
证明:将△APC绕A点逆时针旋转60°,得到△AP′B,连接PP′,则△APP′为等边三角形
∴∠APP′=60° PA=PP′PC=
∵∠APB=150°∴∠BPP′=90°
∴P′P2+BP2=
即PA2+PB2=PC2
(2)类比延伸:
如图②在等腰三角形ABC中,∠BAC=90°,内部有一点P,若∠APB=135°,试判断线段PA、PB、PC之间的数量关系,并证明.
(3)联想拓展:
如图③在△ABC中,∠BAC=120°,AB=AC,点P在直线AB上方,且∠APB=60°,满足(kPA)2+PB2=PC2 , 请直接写出k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年共享单车横空出世,更好地解决了人们“最后一公里”出行难的问题,截止到2016年底,已知“摩拜单车”投放数量有50万辆,“ofo共享单车”的投放数量是“摩拜单车”投放数量的1.6倍,“ofo共享单车”注册用户量比“摩拜单车”的注册用户量多210万人,据统计使用一辆“ofo共享单车”的平均人数比使用一辆“摩拜单车”的平均人数少3人,假设注册这两种单车的用户都在使用共享单车,求2016年“ofo共享单车”和“摩拜单车”的注册用户量各多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
12×231=132×21, 14×451=154×41, 32×253=352×23, 34×473=374×43,45×594=495×54,……
以上每个等式中两边数字是分别对称的,且每个等式中组成两位数与三位数的数字之间具有相同规律,我们称这类等式为“数字对称等式”.
(1)根据上述各式反映的规律填空,使式子成为“数字对称等式”:
①35× = ×53; ② ×682=286× .
(2)设数字对称式左边的两位数的十位数字为m,个位数字为n,且2≤m+n≤9.用含m,n的代数式表示数字对称式左边的两位数与三位数的乘积P,并求出P 能被110整除时mn的值.(其中乘法公式![]() ))
))
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com