
【题目】已知△ABC中,AC=6cm,BC=8cm,AB=10cm,CD为AB边上的高.动点P从点A出发,沿着△ABC的三条边逆时针走一圈回到A点,速度为2cm/s,设运动时间为t s.
(1)求CD的长;
(2)t为何值时,△ACP是等腰三角形?
(3)若M为BC上一动点,N为AB上一动点,是否存在M,N使得AM+MN 的值最小?如果有,请直接写出最小值,如果没有,请说明理由。



【答案】(1) CD=4.8cm;(2) t为6,8.4,9,9.5时,△ACP为等腰三角形;(3)AM+MN的最小值=9.6.
【解析】
(1)根据勾股定理的逆定理得到∠ACB=90°,然后由三角形的面积公式得到等积式,即可得到结果;
(2)①当点P在BC上时,求得t=![]() =6s,②当点P在AB上时,分三种情况:当AC=AP时,即10﹣(2t﹣6﹣8)=6,求得t=9,当AC=CP=6时,即
=6s,②当点P在AB上时,分三种情况:当AC=AP时,即10﹣(2t﹣6﹣8)=6,求得t=9,当AC=CP=6时,即![]() [10﹣(2t﹣6﹣8)]=
[10﹣(2t﹣6﹣8)]=![]() ,求得t=8.4,当AP=CP=10﹣(2t﹣6﹣8)时,即10﹣(2t﹣6﹣8)=5,求得t=9.5;
,求得t=8.4,当AP=CP=10﹣(2t﹣6﹣8)时,即10﹣(2t﹣6﹣8)=5,求得t=9.5;
(3)如图作点A关于BC的对称点A′,过A′作A′N⊥AB于N,交BC于M,′则A′N就是AM+MN的最小值,根据三角形的中位线即可得到结论.
(1)∵AC=6cm,BC=8cm,AB=10cm,∴AC2+BC2=AB2,∴∠ACB=90°.
∵CD为AB边上的高,∴ACBC=ABCD,∴CD=4.8cm;
(2)①当点P在BC上时.
∵∠ACB=90°,若△ACP为等腰三角形,只有AC=PC=6,∴t=![]() =6s;
=6s;
②当点P在AB上时.
∵△ACP为等腰三角形,∴分三种情况:当AC=AP时,即10﹣(2t﹣6﹣8)=6,解得:t=9,当AC=CP=6时,即![]() [10﹣(2t﹣6﹣8)]=
[10﹣(2t﹣6﹣8)]=![]() ,解得:t=8.4,当AP=CP=10﹣(2t﹣6﹣8)时,即10﹣(2t﹣6﹣8)=5,解得:t=9.5.
,解得:t=8.4,当AP=CP=10﹣(2t﹣6﹣8)时,即10﹣(2t﹣6﹣8)=5,解得:t=9.5.
综上所述:t为6,8.4,9,9.5时,△ACP为等腰三角形;
(3)如图作点A关于BC的对称点A′,过A′作A′N⊥AB于N,交BC于M,则A′N就是AM+MN的最小值.
∵CD⊥AB,∴CD∥A′N.
∵AC=CA′,∴AD=DN,∴A′N=2CD=9.6,即AM+MN的最小值=9.6.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出下列四个结论:
①AE=CF;
②△EPF是等腰直角三角形;
③EF=AB;
④![]() ,当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),上述结论中始终正确的有________(把你认为正确的结论的序号都填上).
,当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),上述结论中始终正确的有________(把你认为正确的结论的序号都填上).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( ) 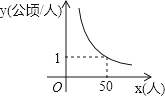
A.该村人均耕地面积随总人口的增多而增多
B.该村人均耕地面积y与总人口x成正比例
C.若该村人均耕地面积为2公顷,则总人口有100人
D.当该村总人口为50人时,人均耕地面积为1公顷
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在太空种子种植体验实践活动中,为了解“宇番2号”番茄,某校科技小组随机调查60株番茄的挂果数量x(单位:个),并绘制如下不完整的统计图表:
“宇番2号”番茄挂果数量统计表
挂果数量x(个) | 频数(株) | 频率 |
25≤x<35 | 6 | 0.1 |
35≤x<45 | 12 | 0.2 |
45≤x<55 | a | 0.25 |
55≤x<65 | 18 | b |
65≤x<75 | 9 | 0.15 |
请结合图表中的信息解答下列问题: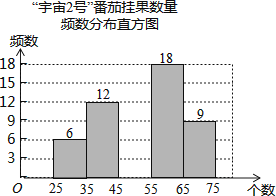
(1)统计表中,a= , b=;
(2)将频数分布直方图补充完整;
(3)若绘制“番茄挂果数量扇形统计图”,则挂果数量在“35≤x<45”所对应扇形的圆心角度数为°;
(4)若所种植的“宇番2号”番茄有1000株,则可以估计挂果数量在“55≤x<65”范围的番茄有株.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC与△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于D.给出下列结论:①AF=AC;②DF=CF;③∠AFC=∠C;④∠BFD=∠CAF.
其中正确的结论个数有. ( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于实数a,我们规定:用符号![]() 表示不大于
表示不大于![]() 的最大整数,称
的最大整数,称![]() 为a的根整数,例如:
为a的根整数,例如:![]() ,
,![]() =3.
=3.
(1)仿照以上方法计算:![]() =______;
=______;![]() =_____.
=_____.
(2)若![]() ,写出满足题意的x的整数值______.
,写出满足题意的x的整数值______.
如果我们对a连续求根整数,直到结果为1为止.例如:对10连续求根整数2次![]()
![]()
![]() =1,这时候结果为1.
=1,这时候结果为1.
(3)对100连续求根整数,____次之后结果为1.
(4)只需进行3次连续求根整数运算后结果为1的所有正整数中,最大的是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的图象如图所示,则一次函数y=ax+b与反比例函数y= ![]() 在同一平面直角坐标系内的图象大致为( )
在同一平面直角坐标系内的图象大致为( ) 
A.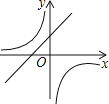
B.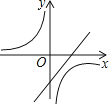
C.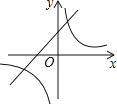
D.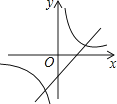
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边三角形ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ, BP=CQ.
(1)求证:△ABP≌△ACQ;
(2)请判断△APQ是什么形状的三角形?试说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com