
【题目】如图所示,折叠长方形一边AD,点D落在BC边的点F处, 已知BC=10厘米,AB=8厘米,求FC和EF的长.
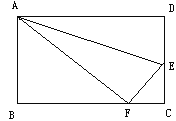
【答案】FC和EF的长分别为4厘米和5厘米.
【解析】
试题由图形翻折变换的性质可知AD=AF,在Rt△ABF中利用勾股定理即可求解得BF的长,再由BC=12厘米可得出FC的长度.设EF=x,由折叠可知DE=EF=x,在Rt△ECF中,由勾股定理得x2=42+(8-x)2,
解得x=5厘米,即EF=5cm.
试题解析:解:折叠长方形一边AD,点D落在BC边的点F处,
所以AF=AD=BC=10厘米;
在Rt△ABF中,AB=8厘米,AF=10厘米,由勾股定理,得
AB2+BF2=AF2
∴82+BF2=102
∴BF=6(厘米)
∴FC=10-6=4(厘米)
设EF=x,由折叠可知DE=EF=x
由勾股定理,得EF2=FC2+EC2
∴x2=42+(8-x)2
解得x=5(厘米)
答:FC和EF的长分别为4厘米和5厘米。


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=120°,AB=AC=4,AD⊥BC,BD=2![]() ,延长AD到E,使AE=2AD,连接BE.
,延长AD到E,使AE=2AD,连接BE.
(1)求证:△ABE为等边三角形;
(2)将一块含60°角的直角三角板PMN如图放置,其中点P与点E重合,且∠NEM=60°,边NE与AB交于点G,边ME与AC交于点F.求证:BG=AF;
(3)在(2)的条件下,求四边形AGEF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:AD平分∠CAE,AD∥BC.
(1)求证:△ABC是等腰三角形.
(2)当∠CAE等于多少度时△ABC是等边三角形?证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
第1个等式:a1= ![]() =
= ![]() ﹣1,
﹣1,
第2个等式:a2= ![]() =
= ![]() ﹣
﹣ ![]() ,
,
第3个等式:a3= ![]() =2﹣
=2﹣ ![]() ,
,
第4个等式:a4= ![]() =
= ![]() ﹣2,
﹣2,
按上述规律,回答以下问题:
(1)请写出第n个等式:an=;
(2)a1+a2+a3+…+an= .
查看答案和解析>>
科目:初中数学 来源: 题型:
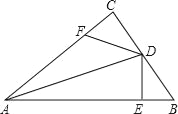
【题目】如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,点F在AC上,且BD=DF.
(1)求证:CF=EB;
(2)请你判断AE、AF与BE之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从①∠1=∠2 ②∠C=∠D ③∠A=∠F 三个条件中选出两个作为已知条件,另一个作为结论所组成的命题中,正确命题的个数为( ) 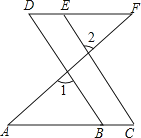
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=kx+b与抛物线y= ![]() x2交于A(x1 , y1)、B(x2 , y2)两点,当OA⊥OB时,直线AB恒过一个定点,该定点坐标为 .
x2交于A(x1 , y1)、B(x2 , y2)两点,当OA⊥OB时,直线AB恒过一个定点,该定点坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用n边形的对角线把n边形分割成(n-2)个三角形,共有多少种不同的分割方案(n≥4)?
(探究)为了解决上面的数学问题,我们采取一般问题特殊化的策略,先从最简单情形入手,再逐次递进转化,最后猜想得出结论.不妨假设n边形的分割方案有Pn种.
探究一:用四边形的对角线把四边形分割成2个三角形,共有多少种不同的分割方案?


如图①,图②,显然,只有2种不同的分割方案.所以,P4=2.



探究二:用五边形的对角线把五边形分割成3个三角形,共有多少种不同的分割方案?
不妨把分割方案分成三类:
第1类:如图③,用A,E与B连接,先把五边形分割转化成1个三角形和1个四边形,再把四边形分割成2个三角形,由探究一知,有P4种不同的分割方案,所以,此类共有P4种不同的分割方案.
第2类:如图④,用A,E与C连接,把五边形分割成3个三角形,有1种不同的分割方案,可视为![]() 种分割方案.
种分割方案.
第3类:图⑤,用A,E与D连接,先把五边形分割转化成1个三角形和1个四边形,再把四边形分割成2个三角形,由探究一知,有P4种不同的分割方案,所以,此类共有P4种不同的分割方案.
所以,P5 =![]() +
+![]() +
+![]() =
=![]() (种)
(种)




探究三:用六边形的对角线把六边形分割成4个三角形,共有多少种不同的分割方案?
不妨把分割方案分成四类:
第1类:如图⑥,用A,F与B连接,先把六边形分割转化成1个三角形和1个五边形,再把五边形分割成3个三角形,由探究二知,有P5种不同的分割方案.所以,此类共有P5种不同的分割方案.
第2类:如图⑦,用A,F与C连接,先把六边形分割转化成2个三角形和1个四边形.再把四边形分割成2个三角形,由探究一知,有P4种不同的分割方案.所以,此类共有P4种分割方案
第3类:如图⑧,用A,F与D连接,先把六边形分割转化成2个三角形和1个四边形.再把四边形分割成2个三角形,由探究一知,有P4种不同的分割方案.所以,此类共有P4种分割方案.
第4类:如图⑨,用A,F与E连接,先把六边形分割转化成1个三角形和1个五边形.再把五边形分割成3个三角形,由探究二知,有P5种不同的分割方案.所以,此类共有P5种分割方案.
所以,P6 =![]() (种)
(种)
探究四:用七边形的对角线把七边形分割成5个三角形,则P7与P6的关系为:
P7 = ![]() ,共有_____种不同的分割方案.……
,共有_____种不同的分割方案.……
(结论)用n边形的对角线把n边形分割成(n-2)个三角形,共有多少种不同的分割方案(n≥4)?(直接写出Pn与Pn -1的关系式,不写解答过程).
(应用)用八边形的对角线把八边形分割成6个三角形,共有多少种不同的分割方案? (应用上述结论,写出解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,AC=6cm,BC=8cm,AB=10cm,CD为AB边上的高.动点P从点A出发,沿着△ABC的三条边逆时针走一圈回到A点,速度为2cm/s,设运动时间为t s.
(1)求CD的长;
(2)t为何值时,△ACP是等腰三角形?
(3)若M为BC上一动点,N为AB上一动点,是否存在M,N使得AM+MN 的值最小?如果有,请直接写出最小值,如果没有,请说明理由。



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com