[题目]直线y=kx+b与抛物线y= x2交于A(x1 . y1).B(x2 . y2)两点.当OA⊥OB时.直线AB恒过一个定点.该定点坐标为．题目和参考答案——青夏教育精英家教网—

【题目】直线y=kx+b与抛物线y= x2交于A（x1 ， y1）、B（x2 ， y2）两点，当OA⊥OB时，直线AB恒过一个定点，该定点坐标为．

【答案】（0，4）
【解析】解：∵直线y=kx+b与抛物线y= x2交于A（x1 ， y1）、B（x2 ， y2）两点， ∴kx+b= ，
化简，得 x2﹣4kx﹣4b=0，
∴x1+x2=4k，x1x2=﹣4b，
又∵OA⊥OB，
∴ ，
解得，b=4，
即直线y=kx+4，故直线恒过顶点（0，4），
所以答案是：（0，4）．
【考点精析】认真审题，首先需要了解一次函数的性质(一般地，一次函数y=kx+b有下列性质：（1）当k>0时，y随x的增大而增大（2）当k<0时，y随x的增大而减小)，还要掌握二次函数的性质(增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小)的相关知识才是答题的关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】如图，花果山上有两只猴子在一棵树CD上的点B处，且BC=5m，它们都要到A处吃东西，其中一只猴子甲沿树爬下走到离树10m处的池塘A处，另一只猴子乙先爬到树顶D处后再沿缆绳DA线段滑到A处．已知两只猴子所经过的路程相等，设BD为xm．

（1）请用含有x的整式表示线段AD的长为______m；

（2）求这棵树高有多少米？

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，等腰三角形ABC的底边BC长为6，面积是18，腰AB的垂直平分线EF分別交AC、AB边于E、F点．若点O为BC边的中点，点M为线段EF上一动点，则△BOM周长的最小值为_______．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图所示，折叠长方形一边AD，点D落在BC边的点F处，已知BC=10厘米，AB=8厘米，求FC和EF的长.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】下列命题中，是假命题的是( )

A. 在△ABC中，若∠A：∠B：∠C＝1：2：3，则△ABC是直角三角形

B. 在△ABC中，若a2＝(b＋c) (b－c)，则△ABC是直角三角形

C. 在△ABC中，若∠B＝∠C＝∠A，则△ABC是直角三角形

D. 在△ABC中，若a：b：c＝5：4：3，则△ABC是直角三角形

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图所示，点O是等边三角形ABC内一点，∠AOB=100°，∠BOC=, D是△ABC外一点，且△ADC ≌△BOC,连接OD.

（1）求证：△COD是等边三角形；

（2）当=150°时，请计算△AOD三内角的度数，并判断△AOD的形状；

（3）探究：当为多少度时，△AOD是等腰三角形？

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，P1、P2是反比例函数y= （k＞0）在第一象限图象上的两点，点A1的坐标为（4，0）．若△P1OA1与△P2A1A2均为等腰直角三角形，其中点P1、P2为直角顶点．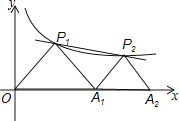

（1）求反比例函数的解析式．
（2）①求P2的坐标．
②根据图象直接写出在第一象限内当x满足什么条件时，经过点P1、P2的一次函数的函数值大于反比例函数y= 的函数值．