
����Ŀ����̫��������ֲ����ʵ����У�Ϊ�˽⡰�2�š����ѣ�ijУ�Ƽ�С���������60�귬�ѵĹҹ�����x����λ�����������������²�������ͳ��ͼ����
���2�š����ѹҹ�����ͳ�Ʊ�
�ҹ�����x������ | Ƶ�����꣩ | Ƶ�� |
25��x��35 | 6 | 0.1 |
35��x��45 | 12 | 0.2 |
45��x��55 | a | 0.25 |
55��x��65 | 18 | b |
65��x��75 | 9 | 0.15 |
����ͼ���е���Ϣ����������⣺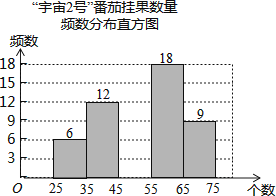
��1��ͳ�Ʊ��У�a= �� b=��
��2����Ƶ���ֲ�ֱ��ͼ����������
��3�������ơ����ѹҹ���������ͳ��ͼ������ҹ������ڡ�35��x��45������Ӧ���ε�Բ�ĽǶ���Ϊ�㣻
��4��������ֲ�ġ��2�š�������1000�꣬����Թ��ƹҹ������ڡ�55��x��65����Χ�ķ������꣮
���𰸡�
��1��15��0.3
��2��
��ͼ��

��3��72
��4��300
���������⣺��1��a=60��0.25=15��b= ![]() =0.3���ʴ��ǣ�15��0.3����2����ȫ��Ƶ���ֲ�ֱ��ͼ����ͼ��ʾ
=0.3���ʴ��ǣ�15��0.3����2����ȫ��Ƶ���ֲ�ֱ��ͼ����ͼ��ʾ  ��
��
��3��������ɵã��ҹ������ڡ�35��x��45������Ӧ���ε�Բ�ĽǶ���Ϊ��360���0.2=72�㣬���Դ��ǣ�72����4��������ɵã��ҹ������ڡ�55��x��65����Χ�ķ����У�1000��0.3=300���꣩��
���Դ��ǣ�300��
�����㾫�����������⣬������Ҫ�˽�Ƶ���ֲ�ֱ��ͼ(�ص㣺��������ʾ�����Ƶ���ֲ��������������ʾ�����Ƶ����𣮣�ע����������ͳ��ͼ��Ƶ���ֲ�ֱ��ͼ��)����Ҫ��������ͳ��ͼ(������ر�ʾ������������������ռ�İٷֱȣ����Dz�������ر�ʾ��ÿ����Ŀ�ľ�����Ŀ�Լ�����ı仯���)�����֪ʶ���Ǵ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���C=90�㣬ADƽ����BAC��DE��AB�ڵ�E����F��AC�ϣ���BD=DF.
(1)��֤��CF=EB��
(2)�����ж�AE��AF��BE֮���������ϵ����˵������.
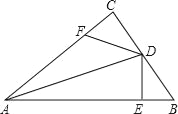
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����OABC�Ķ���O��0��0����B��2��2�����������Ƶ�O��ʱ����ת��ÿ����ת45�㣬���60��ʱ�����εĶԽ��߽���D������Ϊ�������� 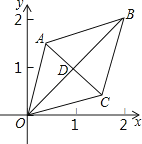
A.��1����1��
B.����1����1��
C.�� ![]() ��0��
��0��
D.��0���� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����B=��C=90 ��M��BC���е㣬DMƽ����ADC.
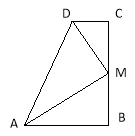
��1��������AM����AM�Ƿ�ƽ����BAD������֤����Ľ��ۣ�
��2���߶�DM��AM��������λ�ù�ϵ����˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ����AC��BC�ǡ�O���ң�ֱ��DE��AC�ڵ�P������D���Ż� ![]() �ϣ�AB=8��BC=3����DP=
�ϣ�AB=8��BC=3����DP=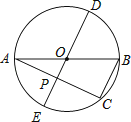
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC�У�AC=6cm��BC=8cm��AB=10cm��CDΪAB���ϵĸߣ�����P�ӵ�A������������ABC����������ʱ����һȦ�ص�A�㣬�ٶ�Ϊ2cm/s�����˶�ʱ��Ϊt s��
��1����CD�ij���
��2��tΪ��ֵʱ����ACP�ǵ��������Σ�
��3����MΪBC��һ���㣬NΪAB��һ���㣬�Ƿ����M��Nʹ��AM+MN ��ֵ��С�������,��ֱ��д����Сֵ�����û�У���˵�����ɡ�



�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��a��0��������������y= ![]() x��ͼ����ͼ��ʾ����ax2+��b��
x��ͼ����ͼ��ʾ����ax2+��b�� ![]() ��x+c=0��a��0��������֮�ͣ� ��
��x+c=0��a��0��������֮�ͣ� �� 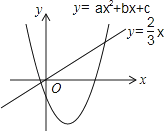
A.����0
B.����0
C.��0
D.����ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��H�ǡ�ABC�ĸ�AD��BE�Ľ��㣬��DH=DC�������н��ۣ���BD=AD����BC=AC����BH=AC����CE=CD����ȷ���У�������

A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������OABC�ı߳�Ϊ4���Խ����ཻ�ڵ�P��������L����O��P��A���㣬��E���������ڵ��������ϵĶ��㣮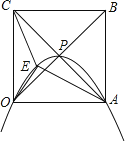
��1�������ʵ���ƽ��ֱ������ϵ��
��ֱ��д��O��P��A�������ꣻ
����������L�Ľ���ʽ��
��2�����OAE���OCE���֮�͵����ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com