
【题目】已知,如图,∠B=∠C=90 ,M是BC的中点,DM平分∠ADC.
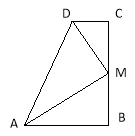
(1)若连接AM,则AM是否平分∠BAD?请你证明你的结论;
(2)线段DM与AM有怎样的位置关系?请说明理由.
【答案】(1)平分;(2)DM⊥AM
【解析】
试题分析:(1)过点M作ME⊥AD于点E,再根据角平分线的性质得到MC=ME,由M为BC的中点可得MC=MB即得ME=MB,再结合MB⊥AB,ME⊥AD即可证得结论;
(2)根据角平分线的性质可得∠ADM=![]() ∠ADC,∠DAM=
∠ADC,∠DAM=![]() ∠BAD,由∠B=∠C=90可得AB//CD,即可得到∠ADC+∠BAD=180,再根据角平分线的性质求解即可.
∠BAD,由∠B=∠C=90可得AB//CD,即可得到∠ADC+∠BAD=180,再根据角平分线的性质求解即可.
(1)AM是平分∠BAD,
理由如下:过点M作ME⊥AD于点E

∵DM平分∠ADC且MC⊥ CD,ME⊥AD
∴MC=ME
∵M为BC的中点
∴MC=MB
∴ME=MB
∵MB⊥AB,ME⊥AD
∴AM平分∠BAD;
(2)DM⊥AM
理由如下:∵DM平分∠ADC
∴∠ADM=![]() ∠ADC
∠ADC
∵AM平分∠BAD
∴∠DAM=![]() ∠BAD
∠BAD
∵∠B=∠C=90
∴AB//CD
∴∠ADC+∠BAD=180
∴∠ADM+∠DAM=![]() ∠ADC+
∠ADC+![]() ∠BAD=
∠BAD=![]() (∠ADC+∠BAD)=90
(∠ADC+∠BAD)=90
∴∠DMA=90
∴DM⊥AM.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
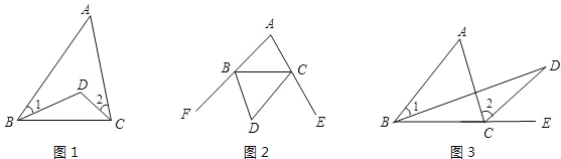
【题目】已知△ABC,(1)如图1,若D点是△ABC内任一点、求证:∠D=∠A+∠ABD+∠ACD.
(2)若D点是△ABC外一点,位置如图2所示.猜想∠D、∠A、∠ABD、∠ACD有怎样的关系?请直接写出所满足的关系式.(不需要证明)
(3)若D点是△ABC外一点,位置如图3所示、猜想∠D、∠A、∠ABD、∠ACD之间有怎样的关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小组7位学生的中考体育测试成绩(满分30分)依次为27,30,29,27,30,28,30.则这组数据的众数与中位数分别是( )
A.30,27
B.30,29
C.29,30
D.30,28
查看答案和解析>>
科目:初中数学 来源: 题型:
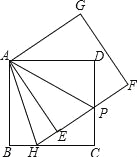
【题目】如图,在边长为6的正方形ABCD中,将正方形ABCD绕点A逆时针旋转角度α(0°<α<90°),得到正方形AEFG,EF交线段CD于点P,FE的延长线交线段BC于点H,连接AH、AP.
(1)求证:△ADP≌△AEP;
(2)①求∠HAP的度数;②判断线段HP、BH、DP的数量关系,并说明理由;
(3)连接DE、EC、CF、DF得到四边形CFDE,在旋转过程中,四边形CFDE能否为矩形?若能,求出BH的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ΔABC中,AB>BC,AB=AC,DE是AB的垂直平分线,垂足为D点,
交AC于点E.
(1)若∠ABE=38°,求∠EBC的度数;
(2)若ΔABC的周长为36cm,一边为13cm,求ΔBCE的周长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com