
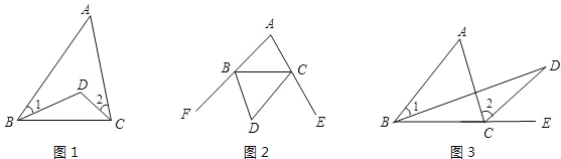
【题目】已知△ABC,(1)如图1,若D点是△ABC内任一点、求证:∠D=∠A+∠ABD+∠ACD.
(2)若D点是△ABC外一点,位置如图2所示.猜想∠D、∠A、∠ABD、∠ACD有怎样的关系?请直接写出所满足的关系式.(不需要证明)
(3)若D点是△ABC外一点,位置如图3所示、猜想∠D、∠A、∠ABD、∠ACD之间有怎样的关系,并证明你的结论.
【答案】(1)证明见解析;(2)∠D+∠A+∠ABD+∠ACD=360°;(3)∠D+∠ACD=∠A+∠ABD,证明见解析.
【解析】试题分析:(1)由∠BDC=∠2+∠CED,∠CED=∠A+∠1,可以得出∠D=∠A+∠ABD+∠ACD.
(2)由∠D+∠A+∠ABD+∠ACD=∠A+∠ABC+∠ACB+∠D+∠DBC+DCB,∠A+∠ABC+∠ACB=180°,∠D+∠DBC+DCB=180°,可以得出∠D+∠A+∠ABD+∠ACD=360°.
(3)根据三角形的外角性质定理即三角形的一个外角等于与它不相邻的两个内角之和,可知∠AED=∠1+∠A,∠AED=∠D+∠2,所以可知∠A+∠1=∠D+∠2即∠D+∠ACD=∠A+∠ABD.
试题解析:(1)证明:延长BD交AC于点E.
∵∠BDC是△CDE的外角,∴∠BDC=∠2+∠CED,
∵∠CED是△ABE的外角,∴∠CED=∠A+∠1.
∴∠BDC=∠A+∠1+∠2.即∠D=∠A+∠ABD+∠ACD.
(2)∵∠D+∠A+∠ABD+∠ACD=∠A+∠ABC+∠ACB+∠D+∠DBC+DCB,
∠A+∠ABC+∠ACB=180°,∠D+∠DBC+∠DCB=180°,
∴∠D+∠A+∠ABD+∠ACD=360°.
(3)证明:令BD、AC交于点E,
∵∠AED是△ABE的外角,
∴∠AED=∠1+∠A,
∵∠AED是△CDE的外角,
∴∠AED=∠D+∠2.
∴∠A+∠1=∠D+∠2即∠D+∠ACD=∠A+∠ABD.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
【题目】某市地铁2号线已开工,全长约332000m,将332000科学记数法表示应为( )
A. 0.332×106 B. 3.32×105 C. 33.2×104 D. 332×103
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A在坐标原点,∠CAB=45°,AC=2![]() ,∠ACB=60°,点B在x轴正半轴,点C在第一象限,动点D在边AB上运动,以CD为直径作⊙O与AC,AB分别交于E,F,连接EF.
,∠ACB=60°,点B在x轴正半轴,点C在第一象限,动点D在边AB上运动,以CD为直径作⊙O与AC,AB分别交于E,F,连接EF.
(1)当△CEF成为等边三角形时,AE:EC= ;
(2)当EF=![]() 时,点D的坐标为 .
时,点D的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列条件中,不能判定四边形是平行四边形的是( )
A. 两组对边分别平行
B. 一组对边平行,另一组对边相等
C. 两组对边分别相等
D. 一组对边平行且相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“六一”儿童节前夕,某幼儿园准备购买彩纸和拼图两种玩具,已知购买1盒彩纸和2盒拼图共需50元,购买2盒彩纸和3盒拼图共需80元.
(1)一盒彩纸和一盒拼图的价格各是多少元?
(2)该幼儿园准备购买这两种玩具共50盒(要求毎种产品都要购买),且购买总金额不能超过850元,至少购买彩纸多少盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,∠B=∠C=90 ,M是BC的中点,DM平分∠ADC.
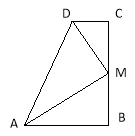
(1)若连接AM,则AM是否平分∠BAD?请你证明你的结论;
(2)线段DM与AM有怎样的位置关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中 ,A(-1,5),B(-1,0),C(-4,3).
(1)请画出△关于y轴对称的△A′B′C′(其中A′,B′,C′分别是A,B,C的对应点,不写画法);
(2)直接写出A′,B′,C′三点的坐标:A′( ),B′( ),C′( );
(3)计算△ABC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com