
【题目】在ΔABC中,AB>BC,AB=AC,DE是AB的垂直平分线,垂足为D点,
交AC于点E.
(1)若∠ABE=38°,求∠EBC的度数;
(2)若ΔABC的周长为36cm,一边为13cm,求ΔBCE的周长.

【答案】(1)33°;(2)23cm.
【解析】试题分析:
(1)由DE是AB的垂直平分线可得AE=BE,从而可得∠A=∠ABE=38°,再由AB=AC就可得∠ABC=∠C=![]() ,最后由∠EBC=∠ABC-∠ABE可得结果;
,最后由∠EBC=∠ABC-∠ABE可得结果;
(2)由已知条件AB>BC,AB=AC可知,当△ABC的周长为36cm时,长为13cm的边只能是腰AB和AC,不能是底边BC,这样可得AB=AC=13,BC=10,再结合(1)中的BE=AE,可求得△BEC的周长为23cm.
试题解析:
(1)∵ DE是AB的垂直平分线,
∴ AE=BE,
∴∠A=∠ABE=38°.
∵AB=AC,
∴∠ABC=∠C=![]() .
.
∴∠EBC=∠ABC-∠ABE=71°-38°=33°.
(2)∵△ABC的周长为36cm,有一边长为13cm,且AB>BC ,AB=AC,
∴AB=AC=13cm ,BC=10cm.
又∵AE=BE,
∴ΔBCE的周长=BE+CE+BC=AE+CE+BC=AC+BC=13+10=23(cm).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A在坐标原点,∠CAB=45°,AC=2![]() ,∠ACB=60°,点B在x轴正半轴,点C在第一象限,动点D在边AB上运动,以CD为直径作⊙O与AC,AB分别交于E,F,连接EF.
,∠ACB=60°,点B在x轴正半轴,点C在第一象限,动点D在边AB上运动,以CD为直径作⊙O与AC,AB分别交于E,F,连接EF.
(1)当△CEF成为等边三角形时,AE:EC= ;
(2)当EF=![]() 时,点D的坐标为 .
时,点D的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,∠B=∠C=90 ,M是BC的中点,DM平分∠ADC.
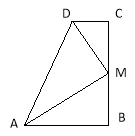
(1)若连接AM,则AM是否平分∠BAD?请你证明你的结论;
(2)线段DM与AM有怎样的位置关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列算式:(1)3a+2b=5ab;(2)5y2﹣2y2=3;(3)7a+a=7a2;(4)4x2y﹣2xy2=2xy中正确的有( )
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D.
(1)求证:△ADC≌△CEB.
(2)AD=5cm,DE=3cm,求BE的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABO中,A,B两点的坐标分别为(2,4),(7,2),C,G,F,E分别为过A,B两点所作的y轴、x轴的垂线与y轴、x轴的交点.求△AOB的面积.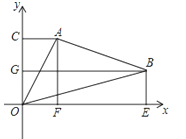
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中 ,A(-1,5),B(-1,0),C(-4,3).
(1)请画出△关于y轴对称的△A′B′C′(其中A′,B′,C′分别是A,B,C的对应点,不写画法);
(2)直接写出A′,B′,C′三点的坐标:A′( ),B′( ),C′( );
(3)计算△ABC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com