
【题目】在等边三角形ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ, BP=CQ.
(1)求证:△ABP≌△ACQ;
(2)请判断△APQ是什么形状的三角形?试说明理由.

科目:初中数学 来源: 题型:
【题目】已知△ABC中,AC=6cm,BC=8cm,AB=10cm,CD为AB边上的高.动点P从点A出发,沿着△ABC的三条边逆时针走一圈回到A点,速度为2cm/s,设运动时间为t s.
(1)求CD的长;
(2)t为何值时,△ACP是等腰三角形?
(3)若M为BC上一动点,N为AB上一动点,是否存在M,N使得AM+MN 的值最小?如果有,请直接写出最小值,如果没有,请说明理由。



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=12厘米, BC=8厘米,点D为AB的中点.如果点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动;当点Q的运动速度为下列哪个值时,能够在某一时刻使△BPD与△CQP全等( )

A. 2或3厘米/秒 B. 4厘米/秒 C. 3厘米/秒 D. 4或6厘米/秒
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,在矩形ABCD中,AB=4cm,BC=7cm,
(1)点F在边BC上,且 BF=3,若点P从点A出发,以每秒1cm的速度沿A→D→C→F运动,设点P运动的时间为t秒,求当t为何值时,△AFP为等腰三角形?




(2)如图2,将长方形ABCD折叠,折痕为MN,点A的对应点A′落在线段BC上,当点A′ 在BC上移动时,点M、N也随之移动,若限定点M、N分别在线段AB、AD上移动,则点A′ 在线段BC上可移动的最大距离是___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形OABC的边长为4,对角线相交于点P,抛物线L经过O、P、A三点,点E是正方形内的抛物线上的动点.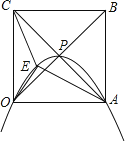
(1)建立适当的平面直角坐标系,
①直接写出O、P、A三点坐标;
②求抛物线L的解析式;
(2)求△OAE与△OCE面积之和的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)作出△ABC关于y轴对称的△ABlCl;
(2)点P在x轴上,且点P到点B与点C的距离之和最小,直接写出点P的坐标为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明想利用太阳光测量楼高.他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:
如示意图,小明边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得小明落在墙上的影子高度CD=1.2m,CE=0.8m,CA=30m(点A,E,C在同一直线上).已知小明的身高EF是1.7m,请你帮小明求出楼高AB.(结果精确到0.1m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知一次函数y=x+3的图象与x轴、y轴分别交于A,B两点,抛物线y=﹣x2+bx+c过A,B两点,且与x轴交于另一点C.
(1)求b、c的值;
(2)如图1,点D为AC的中点,点E在线段BD上,且BE=2ED,连接CE并延长交抛物线于点M,求点M的坐标;
(3)将直线AB绕点A按逆时针方向旋转15°后交y轴于点G,连接CG,如图2,P为△ACG内一点,连接PA,PC,PG,分别以AP,AG为边,在他们的左侧作等边△APR,等边△AGQ,连接QR
①求证:PG=RQ;
②求PA+PC+PG的最小值,并求出当PA+PC+PG取得最小值时点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com