
【题目】已知如图,在矩形ABCD中,AB=4cm,BC=7cm,
(1)点F在边BC上,且 BF=3,若点P从点A出发,以每秒1cm的速度沿A→D→C→F运动,设点P运动的时间为t秒,求当t为何值时,△AFP为等腰三角形?




(2)如图2,将长方形ABCD折叠,折痕为MN,点A的对应点A′落在线段BC上,当点A′ 在BC上移动时,点M、N也随之移动,若限定点M、N分别在线段AB、AD上移动,则点A′ 在线段BC上可移动的最大距离是___________.

【答案】(1)5s,6s,8s,![]() s;(2)(
s;(2)(![]() -3)cm;
-3)cm;
【解析】
(1)利用辅助圆确定点P的位置,再利用等腰三角形的性质判定定理分别确定点P的运动路程,即可得到运动时间;
(2)利用M,N的运动位置确定A′的最大运动位置即可;
解:(1)①如图,以A为圆心,AF长为半径画圆,交AD于![]() ,则AF=A
,则AF=A![]()
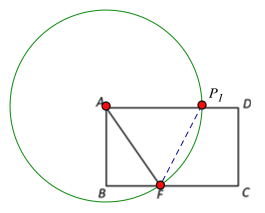
在Rt△ABF中,AB=4cm,BF=3cm,
∴AF=![]() =5cm;
=5cm;
∴AP1=AF=5cm;
∴t1=5s;
∴当t1=5s时,
②如图,以F为圆心,AF长为半径画圆,交AD于![]() ,则FA=F
,则FA=F![]() ,交DC于
,交DC于![]() ,则FA=F
,则FA=F![]()
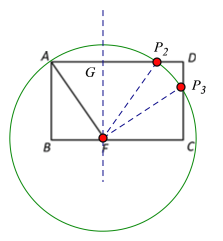
∵BF=3cm, AB=4cm,
∴FA=![]() =5cm;
=5cm;
∴FP2=FP3=FA=5cm,
作FG⊥AD于G,则AP2=2AG=2BF=6cm,
∴t2=6s;
又∵BC=7cm,
∴FC=7-3=4cm,
∴CP3=![]() =3cm,
=3cm,
∴DP3=1cm,
∴AD+DP3=8cm,
∴t3=8s;
③作AF的垂直平分线,交AD于![]() ,交AF于H,连接F
,交AF于H,连接F![]()

∵ABCD为矩形,
∴AD∥BC,∠B=90°,
∴∠DAF=∠AFB,
又∠AHP4=∠B=90°,
∴△AHP4∽△ABF,
![]() ,
,
∴AP4=![]() ,
,
∴t4=![]() s;
s;
综上,当t=5s,6s,8s,![]() s时,△AFP为等腰三角形。
s时,△AFP为等腰三角形。
(2)如图, 当点M与点D重合时, 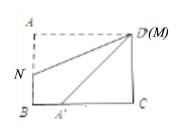
根据翻折对称性可得:DA′=DA=7cm,
在Rt△A′CD中,
A′C=![]() =
=![]() cm,
cm,
如图,当点N与点B重合时,

根据翻折对称性可得BA′=AB=4cm.
∵A′C=CB-BA′,
∴A′C=3cm.
∴点A′在BC边上可移动的最大距离为(![]() -3)cm.
-3)cm.


科目:初中数学 来源: 题型:
【题目】某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( ) 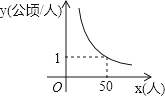
A.该村人均耕地面积随总人口的增多而增多
B.该村人均耕地面积y与总人口x成正比例
C.若该村人均耕地面积为2公顷,则总人口有100人
D.当该村总人口为50人时,人均耕地面积为1公顷
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的图象如图所示,则一次函数y=ax+b与反比例函数y= ![]() 在同一平面直角坐标系内的图象大致为( )
在同一平面直角坐标系内的图象大致为( ) 
A.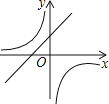
B.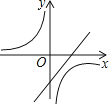
C.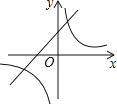
D.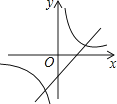
查看答案和解析>>
科目:初中数学 来源: 题型:
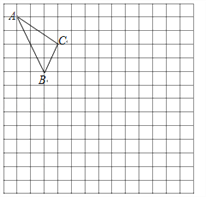
【题目】在如图的正方形网格中,每一个小正方形的边长为1.格点三角形![]() (顶点是网格线交点的三角形)的顶点
(顶点是网格线交点的三角形)的顶点![]() 的坐标分别是
的坐标分别是![]() .
.
(1)请在图中的网格平面内建立平面直角坐标系;
(2)请画出![]() 关于
关于![]() 轴对称的
轴对称的![]() ;
;
(3)请在![]() 轴上求作一点
轴上求作一点![]() ,使
,使![]() 的周长最小,并写出点
的周长最小,并写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为40和28,则△EDF的面积为( )

A. 12 B. 6 C. 7 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角墙角AOB(OA⊥OB,且OA、OB长度不限)中,要砌20m长的墙,与直角墙角AOB围成地面为矩形的储仓,且地面矩形AOBC的面积为96m2 . 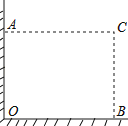
(1)求这地面矩形的长;
(2)有规格为0.80×0.80和1.00×1.00(单位:m)的地板砖单价分别为55元/块和80元/块,若只选其中一种地板砖都恰好能铺满储仓的矩形地面(不计缝隙),用哪一种规格的地板砖费用较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边三角形ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ, BP=CQ.
(1)求证:△ABP≌△ACQ;
(2)请判断△APQ是什么形状的三角形?试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,下列给出四个结论中,正确结论的个数是( )个
①c>0;
②若点B(﹣ ![]() ,y1)、C(﹣
,y1)、C(﹣ ![]() ,y2)为函数图象上的两点,则y1<y2;
,y2)为函数图象上的两点,则y1<y2;
③2a﹣b=0;
④ ![]() <0;
<0;
⑤4a﹣2b+c>0.
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边△ABC的高为6,在这个三角形所在的平面内有一点P,若点P到直线AB的距离是1,点P到直线AC的距离是3,则点P到直线BC的距离可能是_______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com