
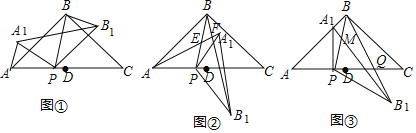
【题目】在△ABC中,AB=BC,∠ABC=90°,D为AC中点,点P是线段AD上的一点,点P与点A、点D不重合),连接BP.将△ABP绕点P按顺时针方向旋转α角(0°<α<180°),得到△A1B1P,连接A1B1、BB1
(1)如图①,当0°<α<90°,在α角变化过程中,请证明∠PAA1=∠PBB1.
(2)如图②,直线AA1与直线PB、直线BB1分别交于点E,F.设∠ABP=β,当90°<α<180°时,在α角变化过程中,是否存在△BEF与△AEP全等?若存在,求出α与β之间的数量关系;若不存在,请说明理由;
(3)如图③,当α=90°时,点E、F与点B重合.直线A1B与直线PB相交于点M,直线BB′与AC相交于点Q.若AB=![]() ,设AP=x,CQ=y,求y关于x的函数关系式.
,设AP=x,CQ=y,求y关于x的函数关系式.
【答案】(1)证明见解析;(2)α﹣2β=90°;(3)y=![]() .
.
【解析】
(1)先利用旋转得出两个顶角相等的两个等腰三角形,即可得出结论;
(2)假设存在,然后利用确定的出AE=BE,即可求出∠A1AP=∠AA1P,最后用∠BAC=45°建立方程化简即可;
(3)先判断出△ABQ∽△CPB,得出比例式即可得出结论.
解:(1)∵将△ABP绕点P按顺时针方向旋转α角(0°<α<180°),得到△A1B1P,
∴∠APA1=∠BPB1=α,AP=A1P,BP=B1P,
∴∠AA1P=∠A1AP=![]() =
=![]() ,∠BB1P=∠B1BP=
,∠BB1P=∠B1BP=![]() =
=![]() ,
,
∴∠PAA1=∠PBB1,
(2)假设在α角变化的过程中,存在△BEF与△AEP全等,
∵△BEF与△AEP全等,
∴AE=BE,
∴∠ABE=∠BAE=β,
∵AP=A1P,
∴∠A1AP=∠AA1P=![]() ,
,
∵AB=BC,∠ABC=90°,
∴∠BAC=45°,
∴β+![]() =45°,
=45°,
∴α﹣2β=90°,
(3)当α=90°时,
∵AP=A1P,BP=B1P,∠APA1=∠BPB2=90°,
∴∠A=∠PBB1=45°,
∵∠A=∠C,∠AQB=∠C+∠QBC=45°+∠QBC=∠PBC,
∴△ABQ∽△CPB,
∴![]() ,
,
∵AB=![]() ,
,
∴![]() ,
,
∴y=![]() .
.


科目:初中数学 来源: 题型:
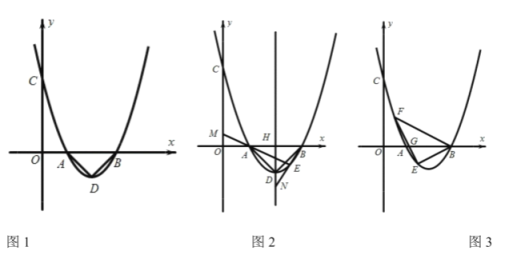
【题目】已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左边),与
的左边),与![]() 轴交于点
轴交于点![]() ,顶点为
,顶点为![]() .
.
(1)如图1,请求出![]() 三点的坐标;
三点的坐标;
(2)点![]() 为
为![]() 轴下方抛物线
轴下方抛物线![]() 上一动点.
上一动点.
①如图2,若![]() 时,抛物线的对称轴
时,抛物线的对称轴![]() 交
交![]() 轴于点
轴于点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,直线
,直线![]() 交对称轴
交对称轴![]() 于点
于点![]() ,求
,求![]() 的值;
的值;
②如图3,若![]() 时,点
时,点![]() 在
在![]() 轴上方的抛物线上运动,连接
轴上方的抛物线上运动,连接![]() 交
交![]() 轴于点
轴于点![]() ,且满足
,且满足![]() 当线段
当线段![]() 运动时,
运动时,![]() 的度数大小发生变化吗?若不变,请求出
的度数大小发生变化吗?若不变,请求出![]() 的值若变化,请说明理由.
的值若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
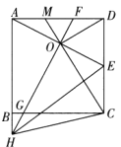
【题目】如图,正方形![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() 的垂直平分线分别交
的垂直平分线分别交![]() ,
,![]() 及
及![]() 的延长线于点
的延长线于点![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() .则下列结论中:①
.则下列结论中:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() .正确结论的个数有( )
.正确结论的个数有( )
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某防洪指挥部发现长江边一处长500米,高10米,背水坡的坡角为45°的防洪大堤(横断面为梯形ABCD)急需加固.经调查论证,防洪指挥部专家组制定的加固方案是:背水坡面用土石进行加固,并使上底加宽3米,加固后背水坡EF的坡比i=1:![]() .
.
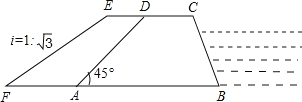
(1)求加固后坝底增加的宽度AF;
(2)求完成这项工程需要土石多少立方米.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为8,E为BC的四等分点(靠近点B的位置),F为B边上的一个动点,连接EF,以EF为边向右侧作等边△EFG,连接CG,则CG的最小值为_____.
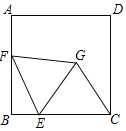
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,在直角边分别为
,在直角边分别为![]() 和
和![]() 的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,依此类推,图10中有
的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,依此类推,图10中有![]() 个直角三角形的内切圆,它们的面积分别记为
个直角三角形的内切圆,它们的面积分别记为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ________.
________.
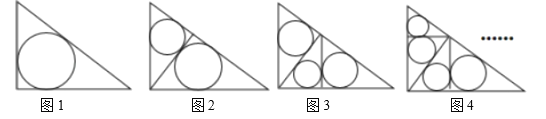
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣![]() x2﹣
x2﹣![]() x+2与x轴交于A、B两点,与y轴交于点C
x+2与x轴交于A、B两点,与y轴交于点C
(1)求点A,B,C的坐标;
(2)点E是此抛物线上的点,点F是其对称轴上的点,求以A,B,E,F为顶点的平行四边形的面积;
(3)此抛物线的对称轴上是否存在点M,使得△ACM是等腰三角形?若存在,请求出点M的坐标;若不存在,请说明理由.
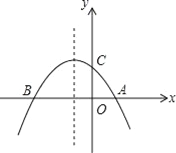
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“六一”儿童节前夕,某部队战士到福利院慰问儿童.战士们从营地出发,匀速步行前往文具店选购礼物,停留一段时间后,继续按原速步行到达福利院(营地、文具店、福利院三地依次在同一直线上).到达后因接到紧急任务,立即按原路匀速跑步返回营地(赠送礼物的时间忽略不计),下列图象能大致反映战
士们离营地的距离![]() 与时间
与时间![]() 之间函数关系的是( )
之间函数关系的是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=kx+b(k≠0)与反比例函数y=![]() (m≠0)的图象相交于A、B两点,且点A的坐标是(1,2),点B的坐标是(﹣2,w).
(m≠0)的图象相交于A、B两点,且点A的坐标是(1,2),点B的坐标是(﹣2,w).
(1)求一次函数与反比例函数的解析式;
(2)在x轴的正半轴上找一点C,使△AOC的面积等于△ABO的面积,并求出点C的坐标.
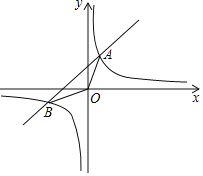
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com