
【题目】如图,正方形![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() 的垂直平分线分别交
的垂直平分线分别交![]() ,
,![]() 及
及![]() 的延长线于点
的延长线于点![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() .则下列结论中:①
.则下列结论中:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() .正确结论的个数有( )
.正确结论的个数有( )
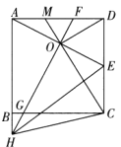
A.2B.3C.4D.5
【答案】B
【解析】
①作辅助线,构建三角形全等,证明△ADE≌△GKF,则FG=AE,可得FG=2AO;
②证明∠HEA=∠AED=∠ODE,OE≠DE,则∠DOE≠∠HEA,OD与HE不平行;
③设正方形ABCD的边长为2x,则AD=AB=2x,DE=EC=x,证明△ADE∽△HOA,得![]() ,所以
,所以![]() ,根据AR∥CD,得
,根据AR∥CD,得![]() ,则
,则![]() ;④证明△HAE∽△ODE,可得
;④证明△HAE∽△ODE,可得![]() ,等量代换可得OE2=AHDE;
,等量代换可得OE2=AHDE;
⑤分别计算HC、OG、BH的长,可得结论.
:①如图,过G作GK⊥AD于K,
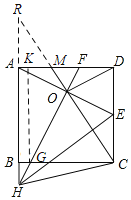
∴∠GKF=90°,
∵四边形ABCD是正方形,
∴∠ADE=90°,AD=AB=GK,
∴∠ADE=∠GKF,
∵AE⊥FH,
∴∠AOF=∠OAF+∠AFO=90°,
∵∠OAF+∠AED=90°,
∴∠AFO=∠AED,
∴△ADE≌△GKF,
∴FG=AE,
∵FH是AE的中垂线,
∴AE=2AO,
∴FG=2AO,
故①正确;
②∵FH是AE的中垂线,
∴AH=EH,
∴∠HAE=∠HEA,
∵AB∥CD,
∴∠HAE=∠AED,
Rt△ADE中,∵O是AE的中点,
∴![]() ,
,
∴∠ODE=∠AED,
∴∠HEA=∠AED=∠ODE,
当∠DOE=∠HEA时,OD∥HE,
但AE>AD,即AE>CD,
∴OE>DE,即∠DOE≠∠HEA,
∴OD与HE不平行,
故②不正确;
③设正方形ABCD的边长为2x,则AD=AB=2x,DE=EC=x,
∴![]() ,
,![]() ,
,
易得△ADE∽△HOA,
∴![]() ,
,
∴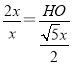 ,
,
∴![]() ,
,
Rt△AHO中,由勾股定理得:![]() ,
,
∴BH=AH-AB= ![]() ,
,
∴![]() ,
,
延长CM、BA交于R,
∵RA∥CE,
∴∠ARO=∠ECO,
∵AO=EO,∠ROA=∠COE,
∴△ARO≌△ECO,
∴AR=CE,
∵AR∥CD,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
故③正确;
④由①知:∠HAE=∠AEH=∠OED=∠ODE,
∴△HAE∽△ODE,
∴![]() ,
,
∵AE=2OE,OD=OE,
∴OE2OE=AHDE,
∴2OE2=AHDE,
故④正确;
⑤由③知:![]() ,
,
∵![]() ,
,
![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴OG+BH≠HC,
故⑤不正确;
本题正确的有;①③④,3个,
故答案为:B.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=a![]() -4ax与x轴交于A,B两点(A在B的左侧).
-4ax与x轴交于A,B两点(A在B的左侧).
(1)求点A,B的坐标;
(2)已知点C(2,1),P(1,-![]() a),点Q在直线PC上,且Q点的横坐标为4.
a),点Q在直线PC上,且Q点的横坐标为4.
①求Q点的纵坐标(用含a的式子表示);
②若抛物线与线段PQ恰有一个公共点,结合函数图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲,乙,丙三人做一个抽牌游戏,三张纸牌上分别写有个数字0,x,y(x,y均为正整数,且x<y),每人抽一张纸牌,纸牌上的数字就是这一轮的得分.经过若干轮后(至少四轮),甲的总得分为20,乙的总得分为10,丙的总得分为9.则甲抽到x的次数最多为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
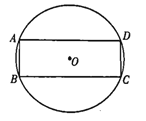
【题目】如图,⊙O为短形ABCD的外接圆,其半径为3.
(1)用尺规作图作出∠ABC的平分线,并标出它与劣弧AD的交点E(保留作图痕迹,不写作法);
(2)若(1)中的点E到弦AD的距离为2,求弦AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】电影《我和我的祖国》上映以来好评如潮,某影评平台随机调查了部分观众对这部电影的评分(满分10分),并将调查结果制成了如下不完整的统计图表(表中每组数据不包括最小值,包括最大值):
等级 | 频数 | 频率 |
A等(9.6分~10分) | a | 0.7 |
B等(8.8分~9.6分) | 3 | 0.15 |
C等(8.2分~8.8分) | b | c |
D等(8.2分及以下) | 1 | 0.05 |
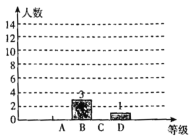
请根据图表信息,解答下列问题:
(1)这次共随机调查了_______名观众,a=______;b=______;c=______;
(2)补全条形统计图;
(3)若某电影院同时上映《我和我的祖国》、《中国机长》和《烈火英雄》,红红和兰兰分别选择其中一部电影观看,求她们选中同一部电影的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=BC,BD⊥AC于点D,∠FAC=![]() ∠ABC,且∠FAC在AC下方.点P,Q分别是射线BD,射线AF上的动点,且点P不与点B重合,点Q不与点A重合,连接CQ,过点P作PE⊥CQ于点E,连接DE.
∠ABC,且∠FAC在AC下方.点P,Q分别是射线BD,射线AF上的动点,且点P不与点B重合,点Q不与点A重合,连接CQ,过点P作PE⊥CQ于点E,连接DE.
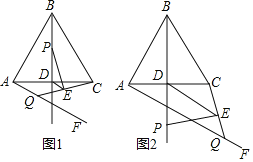
(1)若∠ABC=60°,BP=AQ.
①如图1,当点P在线段BD上运动时,请直接写出线段DE和线段AQ的数量关系和位置关系;
②如图2,当点P运动到线段BD的延长线上时,试判断①中的结论是否成立,并说明理由;
(2)若∠ABC=2α≠60°,请直接写出当线段BP和线段AQ满足什么数量关系时,能使(1)中①的结论仍然成立(用含α的三角函数表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中直线y=x﹣2与y轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2).

(1)求反比例函数的关系式;
(2)将直线y=x﹣2向上平移后与反比例函数图象在第一象限内交于点C,且△ABC的面积为18,求平移后的直线的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
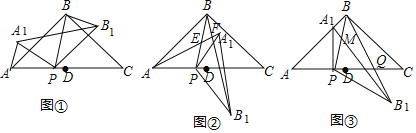
【题目】在△ABC中,AB=BC,∠ABC=90°,D为AC中点,点P是线段AD上的一点,点P与点A、点D不重合),连接BP.将△ABP绕点P按顺时针方向旋转α角(0°<α<180°),得到△A1B1P,连接A1B1、BB1
(1)如图①,当0°<α<90°,在α角变化过程中,请证明∠PAA1=∠PBB1.
(2)如图②,直线AA1与直线PB、直线BB1分别交于点E,F.设∠ABP=β,当90°<α<180°时,在α角变化过程中,是否存在△BEF与△AEP全等?若存在,求出α与β之间的数量关系;若不存在,请说明理由;
(3)如图③,当α=90°时,点E、F与点B重合.直线A1B与直线PB相交于点M,直线BB′与AC相交于点Q.若AB=![]() ,设AP=x,CQ=y,求y关于x的函数关系式.
,设AP=x,CQ=y,求y关于x的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于x的一元二次方程![]() (a≠0)有两个不相等的实数根,且其中一个根为另一个根的2倍,那么称这样的方程为“倍根方程”.例如,方程
(a≠0)有两个不相等的实数根,且其中一个根为另一个根的2倍,那么称这样的方程为“倍根方程”.例如,方程![]() 的两个根是2和4,则方程
的两个根是2和4,则方程![]() 就是“倍根方程”.
就是“倍根方程”.
(1)若一元二次方程![]() 是“倍根方程”,则c=
是“倍根方程”,则c=
(2)若方程![]() (a≠0)是倍根方程,且相异两点M(1+t,s),N(4-t,s),都在抛物线
(a≠0)是倍根方程,且相异两点M(1+t,s),N(4-t,s),都在抛物线![]() 上,求一元二次方程
上,求一元二次方程![]() (a≠0)的根.
(a≠0)的根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com