
【题目】甲,乙,丙三人做一个抽牌游戏,三张纸牌上分别写有个数字0,x,y(x,y均为正整数,且x<y),每人抽一张纸牌,纸牌上的数字就是这一轮的得分.经过若干轮后(至少四轮),甲的总得分为20,乙的总得分为10,丙的总得分为9.则甲抽到x的次数最多为______.
【答案】6
【解析】
根据题意,可得每轮甲,乙,丙得数之和为:x+y,则n轮之和三人得数总和为:n(x+y),所以可得:n(x+y)=39,由n≥4,且n为正整数,可得n=13,x+y=3,根据x,y均为正整数,且x<y,可得x=1,y=2,根据甲的总得分为20,可以设甲a次得0分,b次得x,c次得y,根据题意列方程即可求解.
解:根据题意,每轮甲,乙,丙得数之和为:x+y,
则n轮之和三人得数总和为:n(x+y),
所以可得:n(x+y)=20+10+9=39,
∵n≥4,且n为正整数,而39=3×13,
∴n=13,x+y=3,
∵x,y均为正整数,且x<y,
∴x=1,y=2,
∵甲的总得分为20,
设甲a次得0分,b次得x,c次得y,
则a×0+bx+cy=b+2c=20
∴b=20﹣2c
∴c=![]() (20﹣b)
(20﹣b)
∵0≤c≤13,0≤b≤13,b+c≤13且b,c为正整数,
∴7≤c≤10,0≤b≤6,
所以b最大为6.
答:甲抽到x的次数最多为6.
故答案为:6.


科目:初中数学 来源: 题型:
【题目】如图,点A(﹣2,0),B(0,1),以线段AB为边在第二象限作矩形ABCD,双曲线y=![]() (k<0)过点D,连接BD,若四边形OADB的面积为6,则k的值是( )
(k<0)过点D,连接BD,若四边形OADB的面积为6,则k的值是( )
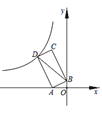
A.﹣9B.﹣12C.﹣16D.﹣18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表,是池州市今年“五一”这周内日最高气温的统计表,关于这7天的日最高气温的众数,中位数,方差分别是:( )
日期 | 29日 | 30日 | 5月1日 | 2日 | 3日 | 4日 | 5日 |
日最高气温 | 16°C | 19°C | 22°C | 24°C | 26°C | 24°C | 23°C |
A. 24,23,10B. 24,23,![]() C. 24,22,10D. 24,22,
C. 24,22,10D. 24,22,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左边),与
的左边),与![]() 轴交于点
轴交于点![]() ,顶点为
,顶点为![]() .
.
(1)如图1,请求出![]() 三点的坐标;
三点的坐标;
(2)点![]() 为
为![]() 轴下方抛物线
轴下方抛物线![]() 上一动点.
上一动点.
①如图2,若![]() 时,抛物线的对称轴
时,抛物线的对称轴![]() 交
交![]() 轴于点
轴于点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,直线
,直线![]() 交对称轴
交对称轴![]() 于点
于点![]() ,求
,求![]() 的值;
的值;
②如图3,若![]() 时,点
时,点![]() 在
在![]() 轴上方的抛物线上运动,连接
轴上方的抛物线上运动,连接![]() 交
交![]() 轴于点
轴于点![]() ,且满足
,且满足![]() 当线段
当线段![]() 运动时,
运动时,![]() 的度数大小发生变化吗?若不变,请求出
的度数大小发生变化吗?若不变,请求出![]() 的值若变化,请说明理由.
的值若变化,请说明理由.
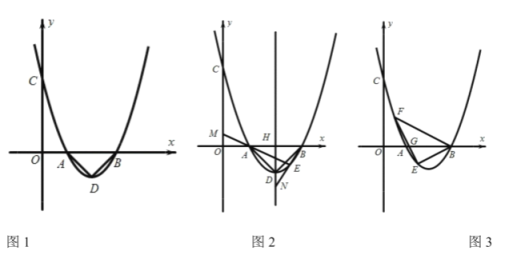
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 与点
与点![]() 关于
关于![]() 轴对称,点
轴对称,点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() 交抛物线于点
交抛物线于点![]() .
.
(1)求点![]() 、点
、点![]() 、点
、点![]() 的坐标;
的坐标;
(2)当点![]() 在线段
在线段![]() 上运动时,直线
上运动时,直线![]() 交
交![]() 于点
于点![]() ,试探究当
,试探究当![]() 为何值时,四边形
为何值时,四边形![]() 是平行四边形;
是平行四边形;
(3)在点![]() 的运动过程中,是否存在点
的运动过程中,是否存在点![]() ,使
,使![]() 是以
是以![]() 为直角边的直角三角形?若存在,求出点
为直角边的直角三角形?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初中数学代数知识中,方程、函数、不等式存在着紧密的联系,请阅读下列两则材料,回答问题:
利用函数图象找方程![]() 解的范围.设函数
解的范围.设函数![]() ,当
,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .则函数
.则函数![]() 的图象经过两个点
的图象经过两个点![]() 与
与![]() ,而点
,而点![]() 在
在![]() 轴下方,点
轴下方,点![]() 在
在![]() 轴上方,则该函数图象与
轴上方,则该函数图象与![]() 轴交点横坐标必大于-2,小于-1.故,方程
轴交点横坐标必大于-2,小于-1.故,方程![]() 的有解,且该解的范围为
的有解,且该解的范围为![]() .
.
材料二:
解一元二次不等式![]() .由“异号两数相乘,结果为负可得:
.由“异号两数相乘,结果为负可得:
情况①![]() ,得
,得![]() ,则
,则![]()
情况②![]() ,得
,得![]() ,则无解
,则无解
故,![]() 的解集为
的解集为![]() .
.
(1)请根据材料一解决问题:已知方程![]() 有唯一解
有唯一解![]() ,且
,且![]() (
(![]() 为整数),求整数
为整数),求整数![]() 的值.
的值.
(2)请结合材料一与材料二解决问题:若关于![]() 的方程
的方程![]() 的解分别为
的解分别为![]() ,
,![]() ,且
,且![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形OABC的两边在坐标轴上,顶点B落在第一象限,反比例函数![]() (x>0)的图象经过正方形OABC的中心P,把反比例函数
(x>0)的图象经过正方形OABC的中心P,把反比例函数![]() (x>0)的图象向左平移a个单位长度后经过点A,若正方形OABC的边长为4,则a的值为( )
(x>0)的图象向左平移a个单位长度后经过点A,若正方形OABC的边长为4,则a的值为( )
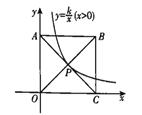
A.![]() B.1C.
B.1C.![]() D.2
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() 的垂直平分线分别交
的垂直平分线分别交![]() ,
,![]() 及
及![]() 的延长线于点
的延长线于点![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() .则下列结论中:①
.则下列结论中:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() .正确结论的个数有( )
.正确结论的个数有( )
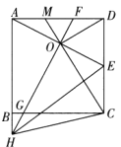
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
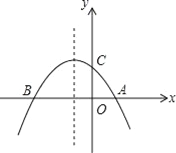
【题目】如图,已知抛物线y=﹣![]() x2﹣
x2﹣![]() x+2与x轴交于A、B两点,与y轴交于点C
x+2与x轴交于A、B两点,与y轴交于点C
(1)求点A,B,C的坐标;
(2)点E是此抛物线上的点,点F是其对称轴上的点,求以A,B,E,F为顶点的平行四边形的面积;
(3)此抛物线的对称轴上是否存在点M,使得△ACM是等腰三角形?若存在,请求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com