
【题目】某地区为筹备一项庆典,利用现有的3490盆甲种花卉和2950盆乙种花卉搭配A,B两种园艺造型共50个摆放在迎宾大道两侧,已知搭配一个A种造型需甲种花卉80盆,乙种花卉40盆;搭配一个B种造型需甲种花卉50盆,乙种花卉90盆,且搭配一个A种造型的成本是200元,搭配一个B种造型的成本是300元,则有多少种搭配方案?这些方案中成本最低的是多少元?
【答案】可设计三种搭配方案, ①A种的造型31个,B种造型19个;②A种造型32个,B种造型18个;③A种造型33个,B种造型17个.由于B种造型的成本高于A种造型成本,所以B种造型越少,成本越低,故应选择方案③,成本最低,最低成本为33×200+17×300=11700(元).
【解析】试题分析:先根据摆放50个园艺造型所需的甲种和乙种花卉应<现有的盆数,可由此列出不等式求出符合题意的搭配方案来,再根据两种造型的成本,得出搭配方案中成本最低的方案,最后计算出成本即可.
试题解析:设搭配A种造型x个,则B种造型为(50-x)个,依题意得![]() 解得31≤x≤33,∵x是整数,∴x可取31,32,33,
解得31≤x≤33,∵x是整数,∴x可取31,32,33,
∴可设计三种搭配方案:①A种的造型31个,B种造型19个;②A种造型32个,B种造型18个;③A种造型33个,B种造型17个.由于B种造型的成本高于A种造型成本,所以B种造型越少,成本越低,故应选择方案③,成本最低,最低成本为33×200+17×300=11700(元)


科目:初中数学 来源: 题型:
【题目】甲乙两队进行足球对抗赛,比赛的规则规定每队胜一场得3分,平一场得1分,负一场得0分.两队一共进行10场比赛,甲队未负一场,得分超过22分.甲队至少胜了多少场?
查看答案和解析>>
科目:初中数学 来源: 题型:
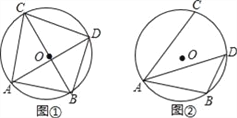
【题目】已知⊙O的直径为10,点A,点B,点C在⊙O上,∠CAB的平分线交⊙O于点D.
(1)如图①,若BC为⊙O的直径,AB=6,求AC,BD,CD的长;
(2)如图②,若∠CAB=60°,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
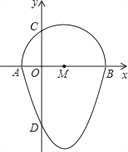
【题目】如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A、B、C、D分别是“果圆”与坐标轴的交点,AB为半圆的直径,抛物线的解析式为y=x2﹣2x﹣3,求这个“果圆”被y轴截得的线段CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0).
(1)若抛物线的顶点是原点,则____________;
(2)若抛物线经过原点,则____________;
(3)若抛物线的顶点在y轴上,则____________;
(4)若抛物线的顶点在x轴上,则____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(方案设计题)某房地产集团筹建一小区,小区内居民楼南北朝向,楼高统一为16 m(共五层).已知该城市冬至日正午时分太阳高度最低,太阳光线与水平线的夹角为32°,所设计的南北两楼之间的距离为20 m(如图所示).
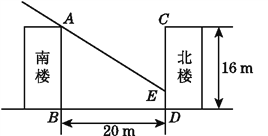
(1)试求出此时南楼的影子落在北楼上有多高;
(2)根据居住要求,每层居民在冬天都要有阳光,请你重新设计一下方案.(结果精确到0.1 m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=ax2+bx+c的图象如图所示,那么关于x的一元二次方程ax2+bx+c-3=0的根的情况是( )
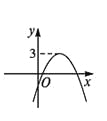
A. 有两个不相等的实数根
B. 有两个异号的实数根
C. 有两个相等的实数根
D. 没有实数根
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com