
【题目】已知x轴上有点A(1,0),点B在y轴上,点C(m,0)为x轴上一动点且m<﹣1,连接AB,BC,tan∠ABO= ![]() ,以线段BC为直径作⊙M交直线AB于点D,过点B作直线l∥AC,过A,B,C三点的抛物线为y=ax2+bx+c,直线l与抛物线和⊙M的另一个交点分别是E,F.
,以线段BC为直径作⊙M交直线AB于点D,过点B作直线l∥AC,过A,B,C三点的抛物线为y=ax2+bx+c,直线l与抛物线和⊙M的另一个交点分别是E,F.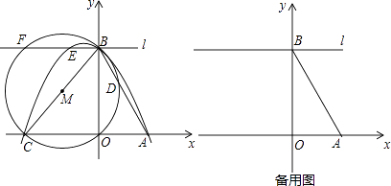
(1)求B点坐标;
(2)用含m的式子表示抛物线的对称轴;
(3)线段EF的长是否为定值?如果是,求出EF的长;如果不是,说明理由.
(4)是否存在点C(m,0),使得BD= ![]() AB?若存在,求出此时m的值;若不存在,说明理由.
AB?若存在,求出此时m的值;若不存在,说明理由.
【答案】
(1)
解:∵tan∠ABO= ![]() ,且A(1,0),
,且A(1,0),
∴OB=2,即:点B的坐标为(0,2)
(2)
解:点C(m,0),A(1,0),B(0,2)在抛物线y=ax2+bx+c上,
∴ 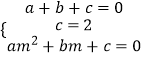
解之得:b=﹣ ![]() ,a=
,a= ![]() ,
,
∴x=﹣ ![]() =
= ![]() .
.
即:抛物线的对称轴为x= ![]()
(3)
解:∵点E在抛物线y=ax2+bx+c上,又在直线y=2上,
∴2=ax2+bx+2
∴x1=0,x2=﹣ ![]()
∴E(﹣ ![]() ,2),
,2),
又∵直线l∥x轴,BC是⊙M的直径,
∴BF∥OC,BF=OC,
∴F(m,2)
∴EF=﹣ ![]() ﹣m,
﹣m,
∵点C(m,0)为x轴上一动点且m<﹣1,
∴m的值是一个变量,
即:线段EF的长不是定值
(4)
解:如下图所示:连接CD
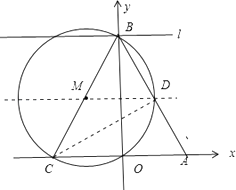
∵BCS是⊙M的直径,
∴∠CDB=90°,
∵若BD= ![]() AB,即BD=DA
AB,即BD=DA
则易证CB=CA
∴ ![]() =1﹣m
=1﹣m
解之得m=﹣ ![]() ,
,
即:存在一点C(﹣ ![]() ,0),使得BD=
,0),使得BD= ![]() AB
AB
【解析】(1)根据正切函数的定义及点A的坐标求解;(2)因为点C、A、B在抛物线上,故代入其坐标列方程组求解即可;(3)点E(x,y)既在抛物线y=ax2+bx+2上,又在直线y=2上,所以有2=ax2+bx+2,由此可知E(﹣ ![]() ,2),又因为直线l∥x轴,BC是⊙M的直径,由圆的对称性可知BF∥OC且BF=OC,所以F(m,2),由此可分析EF长;(4)连接CD,因为BC为圆的直径,所以∠BDC=90°,若BD=
,2),又因为直线l∥x轴,BC是⊙M的直径,由圆的对称性可知BF∥OC且BF=OC,所以F(m,2),由此可分析EF长;(4)连接CD,因为BC为圆的直径,所以∠BDC=90°,若BD= ![]() AB,可证明CA=CB,由此可求得符合题意的点C(﹣
AB,可证明CA=CB,由此可求得符合题意的点C(﹣ ![]() ,0).
,0).


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c与x轴的负半轴交于点A,B(点A在点B的右边),与y轴的正半轴交于点C,且OA=OC=1,则下列关系中正确的是( ) 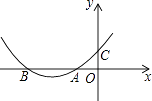
A.a+b=1
B.b<2a
C.a﹣b=﹣1
D.ac<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品公司为指导某种应季商品的生产和销售,在对历年市场行情和生产情况进行调查基础上,对今年这种商品的市场售价和生产成本进行了预测并提供了两个方面的信息:如图(1)(2). 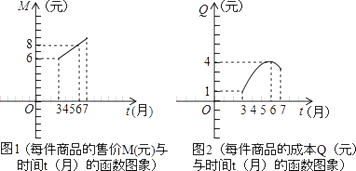
注:两图中的每个实心黑点所对应的纵坐标分别指相应月份一件商品的售价和成本,生产成本6月份最高;图(1)的图象是线段,图(2)的图象是抛物线.
(1)在3月份出售这种商品,一件商品的利润是多少?
(2)设t月份出售这种商品,一件商品的成本Q(元),求Q关于t的函数解析式.
(3)设t月份出售这种商品,一件商品的利润W(元),求W关于t的函数解析式.
(4)问哪个月出售这种商品,一件商品的利润最大?简单说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段AB
(1)请用尺规按下列要求作图:
①延长线段AB到C,使BC=AB,
②延长线段BA到D,使AD=AC(不写画法,当要保留画图痕迹)
(2)请直接回答线段BD与线段AC长度之间的大小关系
(3)如果AB=2cm,请求出线段BD和CD的长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,菱形ABCD的顶点A的坐标为(2,0),点B的坐标为(0,1),点C在第一象限,对角线BD与x轴平行.直线y=x+4与x轴、y轴分别交于点E,F.将菱形ABCD沿x轴向左平移k个单位,当点C落在△EOF的内部时(不包括三角形的边),k的值可能是( )

A.2 B.3 C.4 D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家商店因换季将某种服装打折销售,每件服装如果按标价的4折出售将亏40元,而按标价8折出售将赚40元.问:
(1)每件服装的标价是多少元?
(2)每件服装的成本是多少元?
(3)为了保证不亏损,最多可以打几折?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:小华遇到这样一个问题:
已知:如图1,在△ABC中,三边的长分别为AB= ![]() ,AC=
,AC= ![]() ,BC=2,求∠A的正切值.
,BC=2,求∠A的正切值.
小华是这样解决问题的:
如图2所示,先在一个正方形网格(每个小正方形的边长均为1)中画出格点△ABC(△ABC三个顶点都在小正方形的顶点处),然后在这个正方形网格中再画一个和△ABC相似的格点△DEF,从而使问题得解.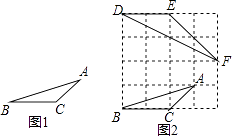
(1)如图2,△DEF中与∠A相等的角为 , ∠A的正切值为 .
(2)参考小华的方法请解决问题:若△LMN的三边分别为LM=2,MN=2 ![]() ,LN=2
,LN=2 ![]() ,求∠N的正切值.
,求∠N的正切值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料1:反射定律
当入射光线AO照射到平面镜上时,将遵循平面镜反射定律,即反射角(∠BOM)的大小等于入射角(∠AOM)的大小,显然,这两个角的余角也相等,其中法线(OM)与平面镜垂直,并且满足入射光线、反射光线(OB)与法线在同一个平面.
材料2:平行逃逸角
对于某定角∠AOB=α(0°<α<90°),点P为边OB上一点,从点P发出一光线PQ(射线),其角度为∠BPQ=β(0°<β<90°),当光线PQ接触到边OA和OB时会遵循反射定律发生反射,当光线PQ经过n次反射后与边OA或OB平行时,称角为定角α的n阶平行逃逸角,特别地,当光线PQ直接与OA平行时,称角β为定角α的零阶平行逃逸角.
(1)已知∠AOB=α=20°,
①如图1,若PQ∥OA,则∠BPQ= °,即该角为α的零阶平行逃逸角;
②如图2,经过一次反射后的光线P1Q∥OB,此时的∠BPP1为α的平行逃逸角,求∠BPP1的大小;
③若经过两次反射后的光线与OA平行,请补全图形,并直接写出α的二阶平行逃逸角为 °;
(2)根据(1)的结论,归纳猜想对于任意角α(0°<α<90°),其n(n为自然数)阶平行逃逸角β= (用含n和a的代数式表示).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com