
【题目】如图,抛物线y=ax2+bx+c与x轴的负半轴交于点A,B(点A在点B的右边),与y轴的正半轴交于点C,且OA=OC=1,则下列关系中正确的是( ) 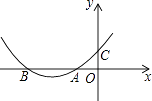
A.a+b=1
B.b<2a
C.a﹣b=﹣1
D.ac<0
【答案】C
【解析】解:A不正确:由图象可知,直线AC:y=x+1,当x=1时,a+b+1>1+1,即a+b>1;
B不正确:由图象可知,﹣ ![]() <﹣1,解得b>2a;
<﹣1,解得b>2a;
C正确:由抛物线与y轴相交于点C,就可知道C点的坐标为(0,c),
又因为OC=OA=1,
所以C(0,1),A(﹣1,0),
把它代入y=ax2+bx+c,
即a(﹣1)2+b(﹣1)+1=0,
即a﹣b+1=0,
所以a﹣b=﹣1.
D不正确:由图象可知,抛物线开口向上,所以a>0;又因为c=1,所以ac>0.
故选:C.
【考点精析】利用二次函数图象以及系数a、b、c的关系对题目进行判断即可得到答案,需要熟知二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】定义:如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.
请解决下列问题:
(1)已知点M,N是线段AB的勾股分割点,且BN>MN>AM.若AM=2,MN=3,求BN的长;
(2)如图2,若点F、M、N、G分别是AB、AD、AE、AC边上的中点,点D,E是线段BC的勾股分割点,且EC>DE>BD,求证:点M,N是线段FG的勾股分割点.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰三角形ABC中,AB=AC=10,BC=12,D为BC边上的任意一点,过点D分别作DE⊥AB,DF⊥AC,垂足分别为E,F,则DE+DF=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
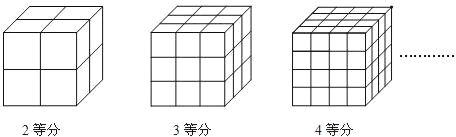
【题目】将一个正方体的表面全涂上颜色.
(1)如果把正方体的棱2等分,然后沿等分线把正方体切开,能够得到8个小正方体,设其中3面被涂上颜色的有a个,则a= ;
(2)如果把正方体的棱三等分,然后沿等分线把正方体切开,能够得到27个小正方体.设这些小正方体中有3个面涂有颜色的有a个,各个面都没有涂色的有b个,则a+b= ;
(3)如果把正方体的棱4等分,然后沿等分线把正方体切开,能够得到64个小正方体.设这些小正方体中有2个面涂有颜色的有c个,各个面都没有涂色的有b个,则c+b= ;
(4)如果把正方体的棱n等分,然后沿等分线把正方体切开,能够得到 个小正方体.设这些小正方体中有2个面涂有颜色的有c个,各个面都没有涂色的有b个,则c+b= .
查看答案和解析>>
科目:初中数学 来源: 题型:
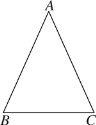
【题目】如图,在△ABC中,AB=AC.
(1)作△ABC的角平分线AD(尺规作图,保留痕迹);
(2)在AD的延长线上任取一点E,连接BE,CE.
①求证:△BDE≌△CDE;
②当AE=2AD时,四边形ABEC是平行四边形吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
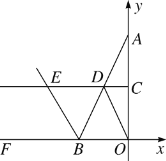
【题目】如图,在平面直角坐标系中,已知点A(0,6),B(b,0),且b<0,C,D分别是OA,AB的中点,△AOB的外角∠DBF的平分线BE与CD的延长线交于点E.
(1)求证:∠DAO=∠DOA;
(2)①若b=-8,求CE的长;
②若CE=![]() +1,则b=________;
+1,则b=________;
(3)是否存在这样的b值,使得四边形OBED为平行四边形?若存在,请求出此时四边形OBED对角线的交点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级全体学生在5名教师的带领下去公园秋游,公园的门票为每人30元.现有两种优惠方案,甲方案:带队老师免费,学生按8折收费;乙方案:师生都按7.5折收费.
(1)若有n名学生,用含n的代数式表示两种优惠方案各需多少元?
(2)当n=70时,采用哪种方案更优惠?
(3)当n=100时,采用哪种方案更优惠?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某的士的起步价为10元(可以坐3千米的路程),若超过3千米,则超出部分每千米另外加收2 元.
(1)小明坐该的士走了x千米的路程,应该付费多少元?
(2)小芳坐该的士走了18千米的路程,应该付费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x轴上有点A(1,0),点B在y轴上,点C(m,0)为x轴上一动点且m<﹣1,连接AB,BC,tan∠ABO= ![]() ,以线段BC为直径作⊙M交直线AB于点D,过点B作直线l∥AC,过A,B,C三点的抛物线为y=ax2+bx+c,直线l与抛物线和⊙M的另一个交点分别是E,F.
,以线段BC为直径作⊙M交直线AB于点D,过点B作直线l∥AC,过A,B,C三点的抛物线为y=ax2+bx+c,直线l与抛物线和⊙M的另一个交点分别是E,F.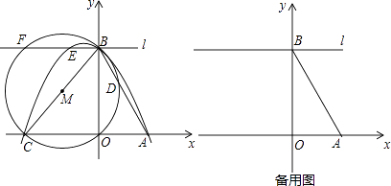
(1)求B点坐标;
(2)用含m的式子表示抛物线的对称轴;
(3)线段EF的长是否为定值?如果是,求出EF的长;如果不是,说明理由.
(4)是否存在点C(m,0),使得BD= ![]() AB?若存在,求出此时m的值;若不存在,说明理由.
AB?若存在,求出此时m的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com