练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在等腰三角形ABC中，AB＝AC＝10，BC＝12，D为BC边上的任意一点，过点D分别作DE⊥AB，DF⊥AC，垂足分别为E，F，则DE＋DF＝______．

    【答案】9.6

    【解析】分析：如图连接AD，作AH⊥BC于H．首先利用勾股定理求出AH，再根据S△ABC=S△ABD+S△ACD，DE⊥AB，DF⊥AC，可得BCAH=ABDE+ACDF，由此即可解决问题．

    详解：如图，连接AD，作AH⊥BC于H．

    ∵AB=AC=10，AH⊥BC，∴BH=CH=6．在Rt△ABH中，AH===8．

    ∵S△ABC=S△ABD+S△ACD，DE⊥AB，DF⊥AC，∴BCAH=ABDE+ACDF，∴6×8=5DE+5DF，∴DE+DF=9.6．

    故答案为：9.6．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知：Rt△ABC中，∠ACB=90°，CA=3，CB=4，设P，Q分别为AB边，CB边上的动点，它们同时分别从A，C出发，以每秒1个单位长度的速度向终点B运动，设P，Q运动的时间为t秒．

    （1）求△CPQ的面积S与运动时间t之间的函数关系式，并求出S的最大值．
    （2）t为何值时，△CPQ为直角三角形．
    （3）①探索：△CPQ是否可能为正三角形，说明理由．
    ②P，Q两点同时出发，若点P的运动速度不变，试改变点Q的运动速度，使△CPQ为正三角形，求出点Q的运动速度和此时的t值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某小组同学在一周内参加家务劳动时间与人数情况如下表所示：

    下列关于“劳动时间”这组数据叙述正确的是（ ）

    A. 中位数是2 B. 众数是2 C. 平均数是3 D. 方差是0

    查看答案和解析>>

    科目：初中数学 来源： 题型：

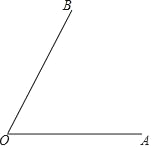
    【题目】如图，∠AOB=60°，分别引射线OC、OD、OE，使OD平分∠BOC，OE平分∠AOD．

    （1）若∠BOC=20°，请依题意补全图形，并求∠BOE的度数；

    （2）若∠BOC=α（其中α是小于60°的锐角），请直接写出∠BOE的度数（用含α的代数式表示）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】△ABC的三边为a、b、c，由下列条件不能判断它是直角三角形的是（　　）

    A. ∠A: ∠B: ∠C =3∶4∶5 B. ∠A=∠B+∠C

    C. a2=(b+c)(b-c) D. a:b:c =1∶2∶

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，点A坐标为（0，3），点B在x轴上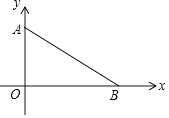
    （1）在坐标系中求作一点M，使得点M到点A，点B和原点O这三点的距离相等，在图中保留作图痕迹，不写作法；
    （2）若函数y= 的图象经过点M，且sin∠OAB= ，求k的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,方格纸中每个小正方形的边长均为1.线段AB的两个端点在小正方形的顶点上。

    (1)在图中画一个以AB为腰的等腰三角形△ABC，点C在小正方形的顶点上，且tan∠B=3；

    (2)在图中画一个以AB为底的等腰三角形△ABD,点D在小正方形的项点上,且△ABD是锐角三角形.连接CD,请直接写出线段CD的长。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=ax2+bx+c与x轴的负半轴交于点A，B（点A在点B的右边），与y轴的正半轴交于点C，且OA=OC=1，则下列关系中正确的是（ ）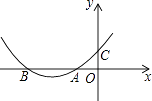

    A.a+b=1
    B.b＜2a
    C.a﹣b=﹣1
    D.ac＜0

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商品公司为指导某种应季商品的生产和销售，在对历年市场行情和生产情况进行调查基础上，对今年这种商品的市场售价和生产成本进行了预测并提供了两个方面的信息：如图（1）（2）．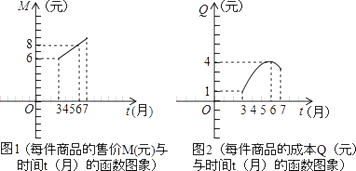

    注：两图中的每个实心黑点所对应的纵坐标分别指相应月份一件商品的售价和成本，生产成本6月份最高；图（1）的图象是线段，图（2）的图象是抛物线．
    （1）在3月份出售这种商品，一件商品的利润是多少？
    （2）设t月份出售这种商品，一件商品的成本Q（元），求Q关于t的函数解析式．
    （3）设t月份出售这种商品，一件商品的利润W（元），求W关于t的函数解析式．
    （4）问哪个月出售这种商品，一件商品的利润最大？简单说明理由．

    查看答案和解析>>

    同步练习册答案