
【题目】如图,已知线段AB
(1)请用尺规按下列要求作图:
①延长线段AB到C,使BC=AB,
②延长线段BA到D,使AD=AC(不写画法,当要保留画图痕迹)
(2)请直接回答线段BD与线段AC长度之间的大小关系
(3)如果AB=2cm,请求出线段BD和CD的长度.
![]()
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
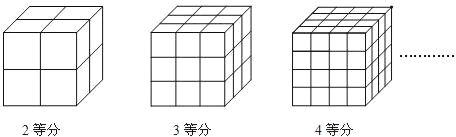
【题目】将一个正方体的表面全涂上颜色.
(1)如果把正方体的棱2等分,然后沿等分线把正方体切开,能够得到8个小正方体,设其中3面被涂上颜色的有a个,则a= ;
(2)如果把正方体的棱三等分,然后沿等分线把正方体切开,能够得到27个小正方体.设这些小正方体中有3个面涂有颜色的有a个,各个面都没有涂色的有b个,则a+b= ;
(3)如果把正方体的棱4等分,然后沿等分线把正方体切开,能够得到64个小正方体.设这些小正方体中有2个面涂有颜色的有c个,各个面都没有涂色的有b个,则c+b= ;
(4)如果把正方体的棱n等分,然后沿等分线把正方体切开,能够得到 个小正方体.设这些小正方体中有2个面涂有颜色的有c个,各个面都没有涂色的有b个,则c+b= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某的士的起步价为10元(可以坐3千米的路程),若超过3千米,则超出部分每千米另外加收2 元.
(1)小明坐该的士走了x千米的路程,应该付费多少元?
(2)小芳坐该的士走了18千米的路程,应该付费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下列填空:
已知:如图,AB∥CD,∠B=120°,CA平分∠BCD.求证:∠1=30°.
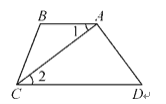
证明:∵AB∥CD( ),
∴∠B+∠BCD= ( ).
∵∠B= ( ),
∴∠BCD= ( ).
又∵CA平分∠BCD( ),
∴∠2= ( ).
∵AB∥CD( ),
∴∠1= =30°( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠B=60°,将△ABC沿对角线AC折叠,点B的对应点落在点E处,且点B,A,E在一条直线上,CE交AD于点F,则图中等边三角形共有( )
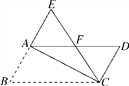
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PB切⊙O于点B,联结PO并延长交⊙O于点E,过点B作BA⊥PE交⊙O于点A,联结AP,AE. 
(1)求证:PA是⊙O的切线;
(2)如果OD=3,tan∠AEP= ![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x轴上有点A(1,0),点B在y轴上,点C(m,0)为x轴上一动点且m<﹣1,连接AB,BC,tan∠ABO= ![]() ,以线段BC为直径作⊙M交直线AB于点D,过点B作直线l∥AC,过A,B,C三点的抛物线为y=ax2+bx+c,直线l与抛物线和⊙M的另一个交点分别是E,F.
,以线段BC为直径作⊙M交直线AB于点D,过点B作直线l∥AC,过A,B,C三点的抛物线为y=ax2+bx+c,直线l与抛物线和⊙M的另一个交点分别是E,F.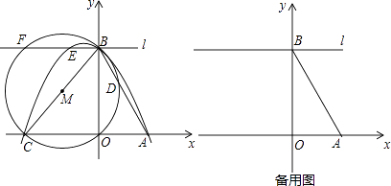
(1)求B点坐标;
(2)用含m的式子表示抛物线的对称轴;
(3)线段EF的长是否为定值?如果是,求出EF的长;如果不是,说明理由.
(4)是否存在点C(m,0),使得BD= ![]() AB?若存在,求出此时m的值;若不存在,说明理由.
AB?若存在,求出此时m的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数y= ![]() 的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO=
的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO= ![]() ,OB=4,OE=2.
,OB=4,OE=2. 
(1)求反比例函数的解析式;
(2)若点D是反比例函数图象在第四象限上的点,过点D作DF⊥y轴,垂足为点F,连接OD、BF.如果S△BAF=4S△DFO , 求点D的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com